Of Men and Machines
By opitts2k
Reality has personality. It is intricate,
complicated, multilayered and consistent. Her consistent nature is of most
importance to mankind as men are hard wired to experience reality through
patterns, logic and continuity. Chaos and disordered things perplex us as our
minds struggle to process the world as a connected continuum with ordered start
and stops, patterns and reasonable existence and purpose. To understand the
nature of reality you must first understand the nature of that thing by which
one observes. The purpose of this text is to offer an approach to understanding
which may be found useful to understanding this reality we call existence.
Reality as we understand it consists of
one totality which is energy that is composed of two distinct motivations we
call forces and matter. It’s not accidental that we consider even the
fundamental properties of existence in terms of a noun and verb. Neither is it
accidental that we describe things as a triad. This is a human construct. Scale
and time is not real and is innately a human construct and therefore relative.
Our biological computer processes the world in chunks, and time and scale is
the minds means to process reality in the frame rates that we understand as
perception. Our description of reality whether described mathematically as
point particles or strings and branes is designed to organize the world by a
set of rules as to prevent the human mind from devolving into a chaotic state.
Ignorance is an untrained mind. Each mind has its own operating procedure set
and must be programmed by its user for optimal performance.
The CPU or Central Processing Unit, system
memory circuits, and IO Devices are the computer. The Motherboard connects and
powers these components of the engineered system. This is true for all
computers including workstations, servers, handhelds and embedded electronics
devices. The CPU is a bit cruncher. From its viewpoint everything is bits. The
CPU is engineered to respond to electrical impulses variation as bits 0 or 1 or
0’s and 1’s bit sequences called bytes or higher aggregates of these computer
voltage patterns. The bit value is 0 or 1. These bytes range in size from bit
to bytes, word sizes and on and on. The CPU's only job is to calculate instruction,
bit or byte by byte, which are voltage, levels encoding and execute these
instruction encodings on a clock cycle. The coding come in
three forms; interpreted executive, address and route.
CPU circuitry is a study in the
disciplines of electricity, material science, and programming theory. These
bits sequences are recognize, addressed and routed by copying bytes, basic
arithmetic tests, bit logic operations and operations that redirect flow like
jump instructions.
A computer CPU starts executing code from
boot firmware, which is a chip on the computer board in from IO device called
ROM (cpu chip). These instructions are called the
BIOS. The BIOS directs CPU to the hard drive (MBR-master boot record section of
the disk), which is a part of the OS (or Operating System). The OS takes over
from there and manages processes to serve the human operator manage the
computer unless its windows 8. Processes ask the operating system via system
calls to be serviced. OS creates a form to manage human to hardware management
via a file system. Os's are Linux, windows, bsd(ox
Mac), and ios, IO devices are managed by devices via device drivers. OS employs
a new addressing scheme called virtual addresses. Virtual addresses are
processed into blocks called pages, which are fed to the processor. Processes
talk to each other via files, pipes, sockets, and signals and shared memory.
Computers are designed to manage one’s
life and modern life is a perception of problem landscapes. These landscapes
can be described by three types of problems pyramid, rugged, and rippling.
Solutions to problems of life require perception; identification,
classification and adaptation to these surfaces for humans traverse the
challenge of living the optimal level of one’s life. Points of a landscape are
solutions and the elevation that point is the value. The number of peaks from
one to many to that of peaks that change with time like rippling water imbues
on the human to constantly adapt and learn to accommodate life for optimal
living. We will call these solution strategies Pyramid, Rugged and Rippling.
Solutions change based on landscape
conditions. Pyramid, rugged and rippling landscape problems are situations,
which have different solutions requirements. For example, a pyramid problem
analogy is what is the optimal rout from home to work in
respect to gas consumption. Calculations may be performed with
increasing relevant variables like gas consumption, mileage and distance and
the fixed problem solution is calculated.
One order higher is the rugged terrain
landscape problems of life. To introduce this next magnitude of order lets
introduce traffic avoidance. This exit or that exit makes the drive a longer
distance but with the payoff of optimal speed and less stop and go for fuel
efficiency of a vehicle is now optimal. The interconnected and interacting
decision of one’s personal choice is a component of complexity but the problem
is not complex yet. It's just complicated. Interaction of ones owns choice and
the consequences of that choice in making route decisions affect the solution
to rugged landscapes problems.
The rippling terrain
landscape problem. To describe this problem, add a police
officer chase with a bag of weed purchased from work. Home has changed because
the police are waiting at the house. Calculate gas consumption to home now.
Well, now the goal of getting home means how much gas to be free because the
solution, optimal gas to home calculation is not home address. Home is freedom
now, which is variable and not ones residence and the complicated
interdependencies of our actions by the actions of others adaptation, since the
police, has been introduced affect the solution. His actions will affect
getting home because the meaning of home, which is necessary for our solution calculation,
has changed. To get home has complexity now because the interdependence on
another's action because of the adaptation of another requires a solution to a
complex problem.
Being human and aware imposes a duality
which must be addressed before we proceed with this text. We are motivated
beings. The idea of world and the earth are different because of our awareness
of experience or sensation of awareness form a historical point of view. The
“world” is us but we exist in the field. The field to date has been a binary
perturbation that is the construct of reality. Our living as a part of the
field and the frame rate reconstruct of reality as awareness should be
considered whenever considering anything to be observed. The fields frame rate
as of the time of this writing is understood by men as the Planck length which
is a measurement derived from three experimental constants, the Planck
constant, universal gravity and the speed of light in a vacuum. Other teachers
consider this construct a primitive view. Having existed for thousands of
billions of years such measurements are fraught with error and a null starter
as light has no absolute speed because there is no absolute measure of time.
Because one day is a thousand years and 1000 years is in reality one day.
The collective of humanity has agreed to
created systems to normalize the uncertainty of life. As beings we abhor
chaotic systems. This abhorrence is experienced psychologically and physically
as biological responses like stress and confusion. Time and scale are tools of
the mind. So it is important to describe the human’s response to these problem
terrains by our description of systems we impose on the world. Systems are
different things working together as a whole. Systems behaviors are classified
as stable, periodic orbits, chaotic, and complex behavior. Stable systems are
observed to repeat the same observed behavior by its parts and therefore the
whole over a period of time. Periodic orbit is a regular sequenced never
changing order of states. Chaotic systems exhibit an initial state of parts and
then unrecognizable or no differentiable classification of parts in the final
observation. Complex behavior is a system that has regular structure like a
periodic system but have longer patterns which require exponentially more
information input to observe more information of the whole.
The goal of the computers was proposed to
organize life into stable complex system. Complex systems are information rich
systems with long intervals. Man’s pursuit of systematization
as a solution of life problems have revealed the following four
observations. Difficult problems require solutions, which are peaks in a rugged
landscape because of the interactions between choices of the same entity in a
rugged landscape. Complex systems survival requires adaptation and learning of
rippling landscapes to survive the interdependency between actions of different
entities adaptation of the respective parties. Interdependence, connectedness,
diversity and adaptation and learning are the tools humans must understand to
control the perils of monotony and chaos. The goal is a stability and richness
through solutions to complex problems. In reality the purpose of these systems
are only to control humanity as will be explained later in the text.
Computers handle varies processes. The
objective of managing these processes for the user is to give cues that humans
understand so that the machine can perform useful operations for the users. The
computer is a tool designed to display visual cues to yield its control and
extend human capability like any other human tool. This is achieved by giving
the human mental cues such as context, continuity and conveyance (the 3 C's).
Continuity is the sense of use which is not operations not changing when same
actions are applied same results occurs. The conveyance aspect
of the user interface are the cues which alerts a user where to go to do
what with the computer interface. Context communicated when and where to
perform a particular user action. For example, the keyboard prompts human to
touch not stare (context); the screen shows the input entered. The file system
whether denoted by slashes or folder icon says something is here, and inside
and above, click me or type (conveyance). These cues to perform actions are the
same everywhere (continuity). This gives the human the illusion of control.
These design consideration for user interaction with computers in a study in
itself in a guide called the human interface guidelines.
Programming a computer consists of
entering commands either visually or lexically into a computer to perform a
task. Not everything done on a computers interface is programming it. Coding a
machine evolves entering instructions for the computer to follow. Various
strategies are used to code computers over the years. Today, text editors
accept coding commands and convert those commands into machine executable
instructions.
Computer operation is based on practices,
conventions and rules devised by engineers and scientist to provide services to
the user. Desktop applications, services and protocols thread in continuum to
maintain the integrity of human computer and computer to human interaction. The
fundamental conventions of computers are database, presentation, and
communication or DPC. Databases expand the human's capacity to organize people
and things. Presentation engages the human with cues and communication extends
the reach of the presentation to others, which promotes sharing to aid
integrity though social interaction.
The computer and the brain are different
types computing tools, which operate on electricity essentially the same but
are structured differently. The computer was designed to handle the extension
of the human's modern day limitations. Humans have not yet discovered practical
ways to exist with infinite strength, time and cognizance. Computers are an
attempt in a relieving these limitations. The computer and the brain are both
machines that operate on electricity but how and why they operate differs
dramatically as of this date. A computer can be fitted with peripherals to
detect and process many of the known environmental external stimuli as a human
brain and can exist practically forever, be fitted with powerful extensions and
can assists the brain in achieving improved omniscience. The brains
construction is based on chemical processes which obeys encoding and stimuli of
over millions if not billions of years of experience and adaptation and is a
gift, and the consensus is that this tool, which is not understood because we
didn't design it, is fraught with simultaneously incredible and feeble
conventions which are unacceptable to humans need for god like presence,
omnipotence and control.
Its architecture inhabits an environment
with a different variable set then that of the computer toolset was designed to
process. The organ has layers of bioelectric networks of nodes called neurons.
The ability for storage is limitless. These nodes are woven together to create
through the process of emergence an experience of mind and continuous
awareness. The organ receives, the mind conceives and our consciousness
perceives. These perceptions have been shown to be helpful, erroneous, and
iterative and helplessly subject to bias, predispositions and limited scope.
The choices are an algorithm followed which can only be changed by changing the
how to conceive. This change is called learning. Factors like interpersonal
handicaps, environmental impediments and disease of the brain can render the
entire system to fail to various degrees. Even to the point of death of the
whole. Here are some examples of errors of CRP:
To leverage the capacity of a tool the
user must understand the range of potential of self as a tool. The tool is an
extension of self. The only purpose of tools are to
maximize leverage of self. Humans have the ability to engage reality as it is.
To date the best understanding of reality is a field. Our existence in the
field permits us limitless interactivity and manipulation of that field. The
field is timeless and it simply has always existed and humans exist in it. We
are beings in this field and we are not the only beings which are a part of the
field. The key to dealing with tools made by men is to understand the
difference between fallacies often promulgated by men and what is real. In this
reality there are many beings of various dimensional strata.
The recognition of cues is critical to
survival in modern society. There is an army of agents guiding society by
intercepting conception to manipulate perception with cues to control human
behavior. The location in the field is not the cues but perception regarding
cues. Cues are any messages that are received by the being in its entirety.
They can be local or non-local because of the duality of body and mind in the field.
All messages come from the brain and non-local messages are the messages from
the field. The mind has quantum properties that are neither dependent on
location nor time. We encapsulate this reality with concepts like technology,
virtual particles, imagination, imaginary numbers and logic but in the past we
called them magic, angels, and divinity. Changing of the name is a political
technique employed to manipulate the perception of the masses. There are
non-local messages.
Computers are counting tools. Before
mechanical computers before World War I was a term to describe humans who
calculated mathematical tables. William Shanks 1900 calculate pi to 27 places.
There have been a myriad of mechanical tools to aid humans in computation. The
abacus rod, Abacus Beads and rods, Hindu Arabic System 4 AD, and the Red Stone
were created 70,000 years ago. American Native Indians used Quipu Ropes and
Knots.
As the modern society grew, the need to
account for society grew. People had to be counted to provide services and thus
were taxed. Farming zones where created and the measure of output needed to be
calculated for grain output. Mathematicians were employed to do very important
calculations for Lords, Kings and Presidents as well. One such mathematician
created the binary counting system. His name was Got fried Wilhelm Leibniz
(1646-1716). As with many mathematical pursuits were solutions looking for a
problem as well as problems looking for a solution. The Jacquard Loom was
developed in France. It was a mechanically programmable scroll through an
apparatus, which mechanically reads hole and changed loom position to change
color and repetition to create design. The loom's card system was adapted to
calculate and reprogram a mechanical calculator by Charles Babb age. Babb age
used this calculator when chartered by the astronomical society to calculate
tables for stars. Babb ages different engine 1822 had a printer Reprogram able
with punch cards also sported a reprogrammed mechanical apparatus to store
calculations. Analytical engine, Ada countess of Lovelace designed software for
the machine. The machines design was rejected and was finally built more 100
years later in the '80s and it worked.
With the Industrial Revolution 1760 to
sometime between 1820 and 1840 started in Britain and within a few decades
spread to Western Europe and the United States need many reliable calculations
for ship navigation, surveying, astronomy, civil engineering and mechanical
engineering and of course politics. Human computers had to use tools like
rulers and tables to perform large calculations. In America human computers
were running short for the first world ware. The Military depended on ballistic
tables to shoot missiles over the horizon. Herman Goldstein was charged with
computing these tables. They had to be reset for weather conditions by K Mokely
to complete the calculation for missile trajectories. Eighteen hundred tables
were required with an adding machine 4 years to do one set of firing tables.
Something happened in the 1930’s. New
ideas were introduced into the science and the military that changed the way
computing and thinking had occurred in the past thousands of years of recorded
history. This influence can be inferred from the results we have witnessed from
then until now. Since that time in the thirties, technology has changed from
procedural layering of conventions and constructs to impose a system. To an
object oriented top down paradigm of using the until
then hidden intricacies of reality to do the will of the engineer. It’s was a
paradigm shift. Somehow humankind discovered, rediscovered or where introduced
to the nature of unseen forces which guide the knowable phenomena observed on
this earth by minds like Newton.
Captain Herman goldstone,
John Moakley & J proper effort. 1800 vacuum
tubes to do a computer. The process were argues and error prone. Then a break
through occurred in the 1930’s. Between 1935-1945 Konrad
Zeus, a civil engineer was introduced to telephones relays, which had on
off switches. The binary system could be used to compute using these relays.
Switched can now be used to count. Using
telephone switched and discarded roles of movie film to code the binary on off.
Just to add 1 and 1 takes four relays. He devised a Programmable general-purpose
computer that takes 3 to 5 seconds to do multiplication. But the switches were
too slow. But as history show all too often, luck is import aspect of
innovation, breakthroughs and successful revolution. Fact about it, the Vacuum tubes were being
developed for radio amplification at the time and were also known for being
extra fast switches. Helmut Schrier approached Conrad and said you could
calculate faster. In the phone electromagnetic relays moving metal from on
contact to another, a metal rod moved up and down. In a vacuum tube electrons
did the switching. Turning on a current was 2000 times faster. German high
command turned them down for funding. This is another import aspect of
innovation, rejection. Electrons were used for the first time to do computing.
Over 50X30 ft. half a million solders joints were needed to make the new system
work.
This groundbreaking work led to the
creation of the ENIAC. Which touted the ability 5000
additions a second. Reprogramming the ENIAC took rewiring by people.
6000 switched and then hundreds of cables. Each accumulator each switch in
front would active and deactivate in the back. John Vonohman joined the team
and wrote a paper to describe for future generations of the computer. He
described a design architecture for an electronic digital computer with
subdivisions, processing unit consisting of an arithmetic logic unit and
processor registers, a control unit containing an instruction register and
program counter, a memory to store both data and instructions, external mass
storage, and input and output mechanisms.
While the ENIAC was a government sponsored
war machine used to decrypt the Germans secret codes. Eckert & Moakley
started a commercial computer companies for private industry. In 1946, Ekert
& Mackley Computer Company built the UNIVAC, which had magnetic tape. The
computer relied on punch cards, keypunch machines and sorters and tabulators
and printers. Armies of clerks shuffled shit everywhere. The US census bureau
was the first candidate. They were drowning in punch cards. They had a census
coming and they needed a computer because congress gave them a time to do it as
mandated by congress. Univac was the name of the new computer. They got swamped
and got hemmed in a fixed cost contract at a fix time. Freddy Williams 1948
created a computer with a first electronically programmable for the endeavor.
The company was a bust thought the job got done.
Across the pond in Britain Morris Wilks,
later left, as he wanted to make a friendly computer called the Edsack for
radio astronomy. In 1951 used the EDSAC to compress three years of work of
Lions electronic offer (LEO), 7 hrs. Rather than in 200 weeks
to do. For the J Lions Company in Britain for
inventory control, payroll and invoices.
Now Alan Touring was a giant of a man. A
homosexual and a genius, his landscape was different than most. In 1936 he
published a paper that described how
Computers could do many of the things that
humans did at the time. He was beyond his time and his dreams were realized
today as he predicted and wrote papers on how the computer could do what they
were doing today and that was replace people. He started manipulating text
letters with the computer. The Germans used an Enigma Lorenz, in cryptogram.
Touring built the colossus computer, which broke the code. Colossus was built
at the same time as the ENIAC. A computer that could solve any task described
with symbols.
The private computer wars had begun in
1950 with the IBM 650 Watson computer vs. Remington Rand (UNIVAC). Software
became increasingly important to control the increasing electronic programming
interface to computers. Fortran was the first
programming language for science it appeared in October 1956. It was later
adopted for business and supplied a compiler.
Around this time another breakthrough
occurred. Bratton Bardine and Scholy created the transistor, which miniaturized
everything. All these tubes and wired created a situation called the tyranny of
numbers. A nest of wired and heat and huge rooms housed computers at this time.
Later in the '50s another breakthrough. Jack Hildon
and Robert Noice discovered the IC or interpreted circuit although Texas
Instruments and Fairchild took credit for it. In 1960 Apollo space flight used
small computer utilizing IC technology to maneuver the spacecraft on the moon.
But for now most working computers were still too big. Connecting them became
an issue. In 1957 a remote connection had to be installed to computers at
DARPA. and timesharing was developed in October the
4th of 1957 to help alleviate the need for onsite computation access.
Remote connectivity was a means to
increase computation presentation in desperate location and non-to soon as a
new threat was on the horizon which would create a need for more computation
and corroboration. The Cold war of 1957 prompted Eisenhower to create the
Bureau and the Defense Department called ARPA (the advanced research projects
agency) he was in charge of the space program, which then included computers,
and a space program to compete with the Russians Sputnik. The US started its
own space computer agency NASA research that went on in relative obscurity.
America turned its attention to conquering the stars and beating the Russians
to space. Other agencies popped up like DARPA US in 1958 and ARPANET
1966(Defense advance research project). A Military network called RAND was
created and a commercial network NPL (NATIONAL PHYSICAL NETWORK) England and
Scientific network CYCLADES) France joined Uncle Sam in it efforts to computer
supremacy. While all these computers networks where in need of being connected
American discover the middle and long range missiles in Cuba, which were able
to reach the United States. These systems were mostly centralized and needed
network architecture to avoid breakdown during the attack ultimately led
decentralized network architecture had to be developed which in case of loss of
a node so that the whole would still be operate. Radio communication through
radio waves at that time would've been ineffective in case of atomic attack.
Radio is ineffective under atomic attack because the ionosphere would be
affected. A long-range solution model with interference was needed.
MIT had the answer. The engineer was
Leonard Klein and he began his qu-ing theory. Packages of data would cue or
line up at the nodes of a communication network every switch, demand access and
distributed control. Circuit switching that telephone systems use of the
technology would depart from computers. The Achilles' heel of this system was
the connection between telephones lines if broken. This
potential loss that was a weakness, which became a matter of national security
to the military in the early 60s when they feared a Soviet nuclear attack on
American cities. We needed an indestructible network.
Paul Boran was hired to see if we could be
built it. He devised hot potato routing for message to transit the network and
go to where it was going node by node. Boren was inspired by previous studies
of mice in a maze. Engineer Claude Shannon in 1952 built a machine that model
mouse finding his way through a maze of secularism. Boran posited that if we
could move a mouse through a maze that we should be able to do the same with
information. Information flows through as encoded packets with encoding
necessary to find its way through the network. Borrowing an idea from the
telegraph Boran decided to chop up each message into small equal sized pieces
called a packet and each was like a postcard with a two and a from address.
Each node knows where it's going and each switch knows how to route to another
switch.
In the 1960s local and wide area networks
did not yet exist. Mainframes were typically “networked” to a series of dumb
terminals with serial connections running on RS-232 or some other electrical
interface. If a terminal in one city needed to connect with a mainframe in
another city, a 300-baud long-haul modem would use the existing analog Public
Switched Telephone Network (PSTN) to form the connection. By 1962 there was
enough research and theory to show that a viable computer network could be
built but implementing it had to wait seven years until 1969 coincidentally the
same year man first walked on the moon. While the space was dominated by
Soviets the first computer network stem from the frustrations of a single
scientist. ARPA scientist Bob Taylor. In 1969
timesharing was the norm. Also, people often paid for computer use back then by
the hour.
When you actually sat at a terminal and
you would type in questions and programs and answers would come back 2 seconds
later. He was at guard at a terminal in 1960s Ex-Taylor of ARPA Advanced
Research Projects Agency Needed a separate Terminal to Log into Each of Several
Timesharing Computers and Research Centers across the Country and No Two
Computers Could Talk to You so Taylor Have To Move from Terminal to Terminal to
Work on a Different Computer and Puts Clients All the Computers Were in the
Floor Taylor Wanted to Build a Network Which Would Link Heterogeneous Computers
to Each Other through This Network called remote sharing. Taylor Recruited
Larry Roberts. Who's first Connection between two computers? MIT
and Lincoln Laboratory's. Built the First 1930 Packet Switching Enjoy
Posting and so I Open the Connection between the Two Computers. Tie Each
Timesharing Computer to a mini computer. Roberts asked 140 Companies Including
AT&T and IBM to Bid on the Project but the Giants of Communication and
Computers Refused.
Larry Roberts Sought out the Engineers to
Build the Advanced Research Projects Agency's Computer Network the ARPANET. It
Was Going to Be Based on Special-Purpose Minicomputers Called Interface Message
Processor (IMP). Small computers (IMP) sat in front of the mainframe
controlling network connectivity.
Support Imps and a Revolutionary Technology Called Packet Switching.
Packets Management for a Bit Trying to Find Its Way to Its Destination Each for
Operating Independently and Final Destination Is Listed As Postcards Carrying
the Data Systems after the Wrong Document and Present for the Recipient Had the
Other the Plan Was to Network for Identical Imps Each One Was Actually
Different Kind of Mainframe Computer Sigma 7 at UCLA, a SDS 940 at the Stanford
Research Institute in IBM Three 360/75 at University Of California at Santa
Barbara, and the PDP 10 at the University of Utah Roberts. Right around this
time in 1966, IBM introduced the first disk storage system, which employed 50
metal platters,
each
of which was 2 feet (0.6 meter) wide and had a storage capacity of 5 MB. IBM
created the first floppy disk in 1967. In 1969, Intel Corporation released a
RAM chip that stored 1 KB of information,
which at the time was an amazing feat of engineering.
A Small Cambridge Massachusetts Company
Called Branigan Newman Known As BBN Wasn't Sure Either but They Were Willing to
Try Frank Hart Headed the BBN Team pioneered Relatively Revolutionary Concept
to Put Together a Packet Switching scheme. Graduate Students at Crocker wrote
software for the First Computer Network computer. They solved issues like. How
Do You Stop the Packets from Circulating Forever? Imps Couldn't Retransmit the
Message. Also there was No Guarantee the Mainframe Computers Would Hold up. On
September 1, 1969 and the First Piece of Hardware Created for the Computer
Network. Right around this time in 1969 Dennis Ritchie creates C. The End of
1969 interconnected All Four Sites. If this Primitive Computer Network Failed
the Effort to Network Computers Might've Been Scrapped as Just another Project
beyond the Reach of Current Technology but It Worked in April 1971 the ARPANET
Had 18 Mainframe Computers Hooked into the Network. Bob Metcalf hooked up MIT's
first network. Transferring Data Files among Its Members.
Raymond Tomlinson invented E-Mail. In 1972 the ARPANET Had Fewer Than 25 Sites.
Also right around this time, 1973, Garry Hidall Created Dos.
Networks Emerge Local Area
Networks, Computers throughout Offices and Plans for Wide-Area Networks to Link
Computers across Buildings or Campuses but Each New Network Was like a Foreign
Country Speaking Its Own Language Good Disparate Networks Be Interconnected to
Make Internet Work. Robert E. Kahn, Engineer
1972, invented TCP IP. Robert Elliot "Bob" Kahn is an American
Internet pioneer, engineer and computer scientist, who, along with Vinton G.
Cerf, invented the Transmission Control Protocol and the Internet Protocol. The
Bell telephone
system
conversion to digital circuitry continued during the 1970s and included the
deployment in 1974 of the first digital data service (DDS) circuits (then
called the Data phone Digital Service). DDS formed the basis of the later
deployment
of ISDN and T1 lines to customer premises, and AT&T installed its first
digital switch in 1976. Around the same time Tim Berners-Lee proposed hypertext
system for access to documents at CERN. The system was called www or the World
Wide Web.
The year 1977 also saw the development of
UNIX to UNIX Copy (UUCP), a protocol and tool for sending messages and
transferring files on UNIX-based networks.
An early version of the USENET news system
using UUCP was developed in 1979. (The Network News Transfer
Protocol [NNTP] came much later, in 1987.) Innovation was everywhere.
Homebrew engineers emerged further innovating and improving computer
technology. In 1975 the Altair 8800 was created. It was the first
microcomputer. In 1976 JERRY LAYSON creates a Video game cartridge. Nolan
Bushnell in 1976 Creates Atari. And in 1976 personal computer is made in a
garage by Steve Wozniack. Hayes introduced the first modem in 1977 and 3Com
shipped the first 10 Mbps Ethernet card in 1981.
In 1978 Ben Serp and Bob Con, and Teamed
up to Develop a Set of Rules or Procedures Known As the TCP/IP Protocol That Is
Followed by Different Computer Networks Would Allow Them to Pass the Message
Packets Back and Forth Is: Which Actually Is the Term Used to Describe a Little
Piece of Papyrus. TCP/IP Protocol Enabled the Networks Interconnect Surfing
Could Call the Computer in the Network That Would Know the Protocol and Thus Be
Able to Communicate across Networks the Gateway. 10 Years of Refinement and
Bureaucratic Haggling finally the TCP estimated the preferences of the OSI
reference model and gave way to the TCP/IP protocol standard which guaranteed
compatibility between networks and finally learns creating the incident family
the 28th 1919 the net heartland was removed but the Internet was born. TCP/IP
Was Adopted As the Universal Standard Marking a Milestone in the Development of
the Internet a Common Network of Interconnected Networks.
The convergence of voice, data, and
broadcast information remained a distant vision throughout the 1980s and was
even set back because of the proliferation of networking technologies, the
competition between cable and broadcast television, and the slow adoption of
residential ISDN. New services did appear, however, especially in the area of
commercial online services such as America Online (AOL), CompuServe, and
Prodigy, which offered consumers e-mail, bulletin
board
systems (BBSs), and other services. A significant milestone in the development
of the Internet occurred in 1982 when the networking protocol of
ARPANET was switched from NCP to TCP/IP.
On January 1, 1983, NCP was turned off permanently—anyone who had not migrated
to TCP/IP was out of luck. ARPANET, which connected several hundred systems,
was split into two parts, ARPANET and MILNET.
Also important to the development of
Internet technologies and protocols was the introduction of the Domain Name
System (DNS) in 1984. At that time, ARPANET
had
more than 1000 nodes and trying to remember their numerical IP addresses was a
headache. DNS greatly simplified that process. Two other Internet protocols
were
introduced soon afterwards: NNTP was developed in 1987, and Internet Relay Chat
(IRC) was developed in 1988.
Pei-Yuan Wei created Violawww in 1990.
Violawww was the first functional web browser. The software was later stolen by
Marc Andresen who later created Mosaic. Mosaic later became Netscape.
In 1989 Quantum Computing was theorized.
Today's computers, like a Turing machine, work by manipulating bits that exist
in one of two states: a 0 or a 1. Quantum computers aren't limited to two
states; they encode information as quantum bits, or qubits, which can exist in
superposition. Qubits represent atoms, ions, photons or electrons and their
respective control devices that are working together to act as computer memory
and a processor. Because a quantum computer can contain these multiple states
simultaneously, it has the potential to be millions of times more powerful than
today's most powerful supercomputers. This superposition of qubits is what
gives quantum computers their inherent parallelism. According to physicist
David Deutsch, this parallelism allows a quantum computer to work on a million
computations at once, while you’re desktop PC works on one. A 30-qubit-quantum
computer would equal the processing power of a conventional computer that could
run at 10 earflaps (trillions of floating-point operations per second). Today's
typical desktop computers run at speeds measured in gig flops (billions of
floating-point operations per second).
Quantum computers also utilize another
aspect of quantum mechanics known as entanglement. One problem with the idea of
quantum computers is that if you try to look at the subatomic particles, you
could disturb them, and thereby change their value. If you look at a qubit in
superposition to determine its value, the qubit will assume the value of either
0 or 1, but not both (effectively turning the quantum computer into a mundane
digital computer). To make a practical quantum computer, scientists have to
devise ways of making measurements indirectly to preserve the system's
integrity. Entanglement provides a potential answer. In quantum physics, if you
apply an outside force to two atoms, it can cause them to become entangled and
the second atom can take on the properties of the first atom. So if left alone,
an atom will spin in all directions. The instant it is disturbed it chooses one
spin, or one value; and at the same time, the second entangled atom will choose
an opposite spin, or value. This allows scientists to know the value of the
qubits without actually looking at them.
The purpose of the computer as a tool is
to manage the complexity of human life. The computer plays mathematical formula
like an instrument was designed to play music to a time signature. To perform math operation, by the use of engineering the electronic
internals to signal based timing of a clock. Math is a language just
like English or Spanish. Language is the use of words based on rules to
communicate a thought. There are language rules called, semantics, lexicon and
grammar.
Math is man’s effort to map the world, as
it is perceived by our minds. The average brain has been hardwired to
distinguish two properties and perform generalization. The two properties are
differentiation, and quality of differentiation, these properties are stored as
generalizations which in turn prepares the brain for further differentiation
and so forth. The generalization is a filing scheme, which packs events with
enough cues so that the user can recall. Mathematics is the study of the
measurement, properties, and relationships of quantities, using numbers and
symbols. We also have the capability of abstraction of those concepts and
communicate mathematical language. Men manage needs opposing wants and needs of
other men through a system of society and for that measurement, which is
politically accepted, are needed to survive, control, inhabit and cohabit to
promote the species.
Mathematical Object Types
Type Notation Example
Scalar Lower-case a, b, x, y1
Infinity ∞ +∞, -∞
Angle Lower-case Greek θ, φ,
α, β
Vector Lower-case bold u, v, ax, ay
Quaternion Lower-case bold p, q, rx, sy
Elements of Vector <components>
<ux, uy, uz>
Row Vector [components] [ux, uy, uz]
Point Lower-case bold a, p1, p2
Matrix Upper-case bold A, B, M2
Triangle Δ followed by points
Δp0p1p2, Δabc
Note: All types can be subscripted or
superscripted.
Now that we have a “general” guideline for
types (although I might get
Operation Notation Example
Scalar Multiplication x,* Lower-case 3x5,
a*b
Matrix Multiplication x, Lower-case AxB
Dot Product . u . v
Summation Σ expr
Absolute Value |expr| |-35|
Length |expr| |u|
Determinate det(expr)
det(M)
Transpose Superscript T vT
Integration ∫ expr
Differentiation Prime Symbol ' x', x''
Note: “expr” stands for general
expression.
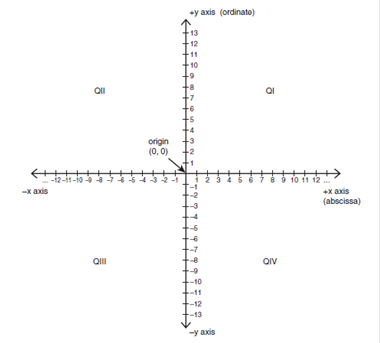
Cartesian System
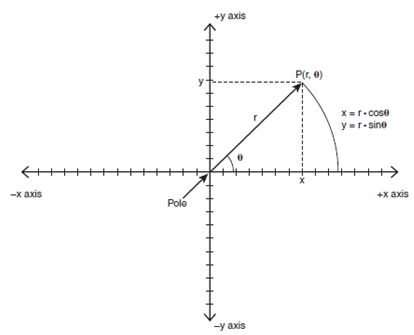
Polar System
Signs in Each Quadrant
Quadrant Sign (x) Sign (y)
I
+ +
II
- +
III
- -
IV
+ -
Radians vs. Degrees
360 = degress = 2*PI radians approx. 6.28
radians
180 degress = PI radians approx. 3.14159 radians
360 degrees / 2*PI radians = 1 radians is approx.
57.296
2*PI radians / 360 degree = 1 degress is
approx. 0.0175
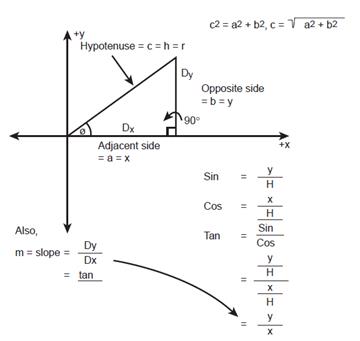
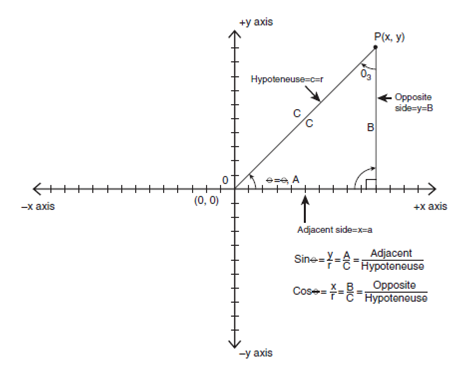
cos(theta)
= adjacent side / hypotenuse = x/r
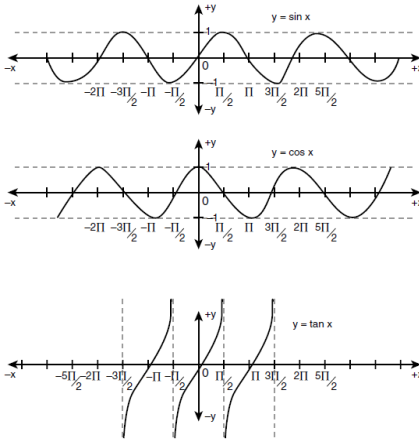
Domain: 0 <= theta <= 2*pi
Range: -1 to 1
sin(theta)
= opposite side / hypotenuse = y/r
Domain: 0<= theta <2*pi
Range: -1 to 1
tan(theta)
= sin(theta)/cos(theta) = opposite/hypotenuse / adjacent/hypontenuse
Useful
Trigonometric Identities
Cosecant
csc
(theta) = 1/sin (theta)
Secant
sec
(theta) = 1/cos (theta)
Cotangent cot (theta) = 1/tan (theta)
Pythagorean Theorem in terms
of trig functions:
Sin
(theta) 2 + cos(theta)2 = 1
Conversion identity:
sin(theta1) = cos(theta1 – PI/2)
Reflection identities:
sin(-theta) = -sin(theta)
cos(-theta) = cos(theta)
Addition identities:
sin(theta1 + theta2) = sin(theta1)*cos(theta2) +
cos(theta1)*sin(theta2)
cos(theta1 + theta2) = cos(theta1)*cos(theta2) -
sin(theta1)*sin(theta2)
sin(theta1 - theta2) = sin(theta1)*cos(theta2) -
cos(theta1)*sin(theta2)
cos(theta1 - theta2) =
cos(theta1)*cos(theta2) + sin(theta1)*sin(theta2)
radius R is computed as
xr = r*cos(theta)
yr = r*sin(theta)
3D System
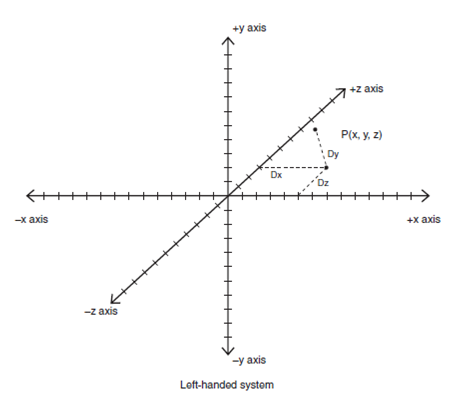
Converting 3D Polar Coordinates p(r,θ,z) to Cartesian Coordinates p(x,y,z)
x = r*cos(θ)
y = r*sin(θ)
z = z
Converting 3D Cartesian Coordinates p(x,y,z) to Polar Coordinates p(r,θ,z)
Given: x2 + y2 = r2
r = sqrt(x2 + y2)
θ = tan-1(y/x)
z = z
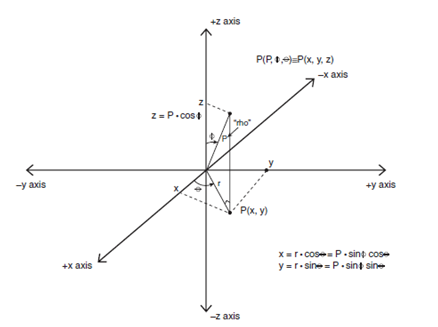
Converting 3D Spherical Coordinates p(ρ,φ,θ) to Cartesian Coordinates
p(x,y,z)
From the projection of the line segment o->p onto
the x-y plane, we see that:
r = ρ*sin(φ)
z = ρ*cos(φ)
and in the x-y plane, we know
that:
x = r*cos(θ)
y = r*sin(θ)
Therefore, substituting r into x,y
and collecting equations gives:
x = ρ*sin(φ)*cos(θ)
y = ρ*sin(φ)*sin(θ)
z = ρ*cos(φ)
Converting 3D Cartesian Coordinates p(x,y,z) to Spherical Coordinates
p(ρ,φ,θ)
Given: x2 + y2 + z2= ρ2
Similarly: x2 + y2 = r2
Therefore:
r = sqrt(x2 + y2)
ρ = sqrt(x2 + y2 + z2)
θ = tan-1(y/x)
And we can solve for φ after we have r and
ρ from the relationship:
r = ρ*sin(φ)
Solving for φ gives:
φ = sin-1(r/ρ)
Also, we can use:
z = ρ*cos(φ)
Therefore:
φ = cos-1(z/ρ)
Radians Versus Degrees
Angle in Degrees Angle in Radians
360 degrees 2*PI radians (approx. 6.28 radians)
180 degrees PI radians (approx. 3.14159 radians)
57.296 degrees 360 degrees/2*PI radians = 1 radian
1.0 degrees 2*PI radians/360 degrees = 0.0175
radians
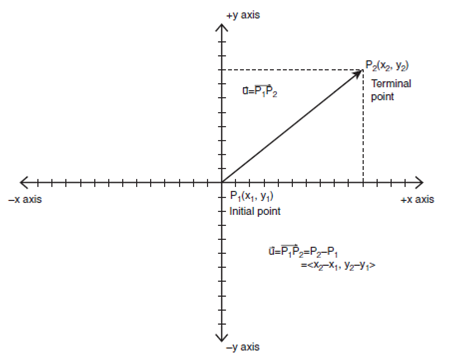
Vector Length
How to compute the length of a vector or its
magnitude. The length of a vector is called the norm and is
represented by two vertical bars on either side of the vector (at least in this
book), such as |u| and read as, “the length of u.” The length is computed as
the distance from the origin to the tip of the vector, or in general as the
square root of the sum of the squares of the components. Hence, we can use the
standard Pythagorean Theorem to find the length in the 2D and 3D case. Hence,
|u| is equal to the following:
The Length of a 2D Vector u = <ux, uy>
|u| = sqrt(ux 2 + uy 2)
And if u happened to be a 3D vector, the length
would be:
The Length of a 3D Vector u = <ux, uy, uz>
|u| = sqrt(ux 2 + uy 2 + uz
2)
Matrixes
A that is 2*2:
A
= |1 4|
|9 –1|
Here’s a 3×2 matrix:
|5
6|
B =
|2 3|
|100 -7|
And here’s a 2×3 matrix:
C =
| 3 5 0 |
|-8 12 4 |
here’s the labeling of a 3×3
matrix:
|a00 a01 a02|
A =
|a10 a11 a12|
|a20 a21 a22|
Basically, a system of
equations like
3*x
+ 2*y = 1
4*x – 9*y = 9
Here are the coefficients:
3*x
+ 2*y = 1
4*x – 9*y = 9
A =
|3 2|
|4 -9|
Dimension
is 2x2
Here are the variables
themselves:
3*x
+ 2*y = 1
4*x
– 9*y = 9
X =
|x|
|y|
Dimension
is 2x1 And finally, here are the
constants to the right:
3*x
+ 2*y = 1
4*x
– 9*y = 9
B =
|1|
|9|
Dimension
is 2x1
With all
these nice matrices, can focus on, say, the coefficient matrix A without
all the other stuff. Moreover, matrix equations like
A*X
= B
The math is
3*x
+ 2*y = 1
4*x
– 9*y = 9
But how to
perform the math?
That’s our next topic.
The
Identity Matrix
The first thing needed to
define in any mathematical system is 1 and 0. In matrix mathematics, there are
analogs of both of the values. The analog of 1 is called the identity matrix
and is created by placing all 1s in the main diagonal of the matrix and 0s
everywhere else. Furthermore, because matrices can be any size, there are
obviously an infinite number of identity matrices. However, there is one
constraint: All identity matrices must be square, or in other words m×m,
where m >= 1. Here are a couple of examples:
I2 =
|1 0|
|0 1|
Dimension 2x2
|1 0 0 |
I3 =
|0 1 0 |
|0 0 1 |
Dimension
3x3
Ironically, the identity
matrix isn’t exactly the analog of 1, but is under matrix multiplication. The
second type of fundamental matrix is called the zero matrix,
and it’s 0 under both addition and multiplication. It’s nothing more than a
matrix of dimension m×n with all entries 0. Other than that,
there are no special constraints:
|0 0 0|
Z3x3
=
|0 0 0|
|0
0 0|
Z1x2
=
|0 0|
The only interesting thing
about the zero matrix is that it has the standard
properties of scalar 0 for both matrix addition and multiplication. Other than
that, it’s pretty useless.
Matrix
Addition
Addition and subtraction of
matrices is performed by adding or subtracting each element in two matrices and
coming up with a result for each entry. The only rule to addition and
subtraction is that the matrices that the operation is being performed on must
be of the same dimension. Here are two examples:
A =
|1 5| B = |13 7
|
|-2 0|
|5 –10|
A +
B = |1 5| + |13
7 | = |(1+13) (5+7)| = |14 12|
|-2 0|
|5 –10| |(-2+5)
(0-10| |3 -10|
A –
B = |1 5| + |13
7 | = |(1-13) (5-7) | = |-12 –2|
|-2 0|
|5 –10| |(-2-5)
(0-(-10))| |-7 10|
Note that both addition and
subtraction are associative; that is, A + (B + C) = (A + B)+
C. However, they’re not commutative under subtraction. (A – B) may not equal (B
– A).
Here’s a general description
for a 3×3 matrix. Let k be any real constant:
|a00 a01 a02|
Let
A = |a10 a11 a12|
|a20 a21 a22|
|a00 a01 a02|
|k*a00 k*a01 k*a02|
Then
k*A = k*|a10 a11 a12| =
|k*a10 k*a11 k*a12|
|a20 a21 a22| |k*a20 k*a21 k*a22|
Here’s an example:
3*|
1 4| = |(3*1)
(3*4)| = |3 12|
|-2 6|
|(3*(-2)) (3*6)| |-6 18|
The sum of
products (1*1 + 2*6). This product and all the others are really vector dot products
(a vector is just a collection of values, like a matrix with one row). A
dot product has a very explicit mathematical meaning, which we’ll get to later,
but in general, to compute the dot product of two vectors that are each 1nth
by simply summing up the products of the independent components. Or,
mathematically:
Let
a = [1 2 3] b = [4 5 6]
a*b =
[(1*4) + (2*5) + (3*6)] = [32]
1x1
Or, just use a scalar.
Scaling
To scale a point relative to
the origin just multiply the x,y components by
scaling factors sx and sy,
respectively. In addition, translation during the scaling
operation. Here’s the matrix needed:
|sx 0 0|
Ms
=|0 sy 0|
|0 0 1|
Eg. p = [x y 1]
|sx 0 0|
p’ = p*Ms = [x y 1] * |0 sy 0| = [(x*sx) (y*sy)
1]
|0 0 1|
Again, this is the desired
result for scaling; that is
x’ = sx*x
y’ = sy*y
Note
the 1 in the lower-right corner of the transformation matrix.
Technically,
it’s not necessary to use the result from the third column. Hence,
increasing the math cycles. The question is, can we remove the last
column of all the transformation matrices and use a 3×2 instead? Let’s see the
rotation matrix before that…
Rotation
The rotation matrix is the
most complex of all the transformations because it’s full of trig functions.
Rotate the input point by using the rotation equations.
To achieve this, look at the
rotation equations, pick the operators, and then push them into a matrix. In
addition, we don’t want any translation, so the bottom row in positions 0 and 1
will be 0. Here’s the matrix that does the job:
| cos × sin × |
Mr
= |-sin × cos × |
| 0
0 1 |
Eg. p = [x y 1]
| cos × sin × |
p’ = p*Mr = [x y 1] * |-sin × cos × | = | 0 0 1
|
p’ = [(x*cos × – y*sin ×) (x*sin × + y*cos ×)
1]
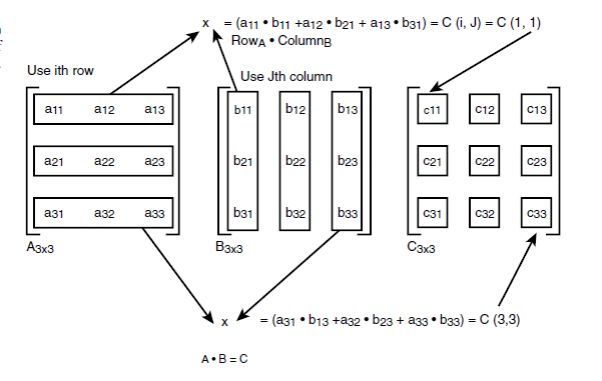
The second type of
multiplication is true matrix multiplication. A matrix is an “operator” that
operates on another matrix. Given two matrices, A and B, that
could be multiplied, they must have the same inner dimension. In other words,
if A is m×n, B must be n×r. m and
r may or may not be equal, but the inner dimension must be. For example,
multiply a 2×2 by a 2×2, a 3×2 by a 2×3, and a 4×4 by a 4×5, but it can’t be
multiply by a 3×3 by a 2×4 because the inner dimensions aren’t
equal. The resulting matrix will have a size that is equal to the outer
dimension of the multiplier and multiplicand matrix. For example, a 2×3
multiplying a 3×4 would have dimension 2×4. Matrix multiplication is one
of those things that’s very hard to describe with
words. The technical description of the multiplication
algorithm. Given a matrix A and B, or A×B,
and to multiply them together to compute each element of the result matrix C,
you must take a row of A and multiply it by a column in B. To
perform the multiplication, the sum of the products of each element, which is
also called the dot product. Here’s an example for a 2×2 multiplying a 2×3
in respect to order!
Let
A = |1 2| B = |1 3 5|
|3 4| |6 0 4|
C =
A x B = |(1*1 + 2*6) (1*3 + 2*0) (1*5 +2*4)|
|(3*1 + 4*6) (3*3 +
4*0) (3*5 +4*4)|
=
|13 3 13|
|27
9 31|
Matrix
Multiplication
There are two forms of
matrix multiplication: scalar and matrix. Scalar matrix
multiplication is simply the multiplication of a matrix by a scalar number.
Multiply each element of the matrix by the number. The matrix can be m×n
at any size.
Introduction to Quaternions
Quaternions were invented in
the 1800s by the mathematician William Rowan Hamilton (or Hamiltonian paths).
Quaternions weren’t specially designed for 3D graphics but they have found
their application in a couple of areas of 3D graphics for which they are well
suited:
• 3D camera control
• Compact storage
• Smooth 3D interpolation
Quaternions are based on
complex numbers. They exist mathematically and complex numbers are a tool that
can be used to represent mathematical ideas for which real numbers just don’t
work. With that in mind, first we are going to take a look at basic complex
number theory, and then move on to quaternions and their mathematical
properties. After that we’ll see how they are applied in computer graphics and
games.
Complex Number Theory
The set of real numbers R
consists of all numbers in the interval [-∞, +∞]:
x = sqrt(4)
= 2
x = sqrt(1)
= 1
x = sqrt(-1)
= ???
The third equation is the
problem that there is no number in the set of real numbers for the square root
of –1 because there is no number that when multiplied by itself
is equal to –1. It could be deduced that its –1, but
–1 * –1 = 1, so that’s not correct. We need a new number, which is called the
imaginary number i (or j for electrical engineers). Here is the rule:
let i = sqrt(-1)
And then
i*i = -1
Now we can compute things
like sqrt(-4), which would be sqrt(-4) = 2*i
The imaginary number i is a
variable or coefficient; that is, all the rules of normal algebra still hold.
Just consider i is a variable like. Then i2 terms, are
converted into –1. For example, look at the following sum:
3 + 5*i + 3*i2 – 10 + 6*i
Collecting terms, we get
= 3*i2 + 5*i + 6*i + 3 – 10
= 3*i2 + 11*i - 7
= 3*(-1) + 11*i – 7
= -3 + 11*i – 7
= -10 + 11*i
Mathematically, a complex
number is a imaginary number and looks like this:
z = (a + b*i)
a is called the real part
(RP), and b is called the imaginary part (IM). Because a and b can never be
added together because of the imaginary coefficient of b, complex numbers are
points in the complex plane, as shown in
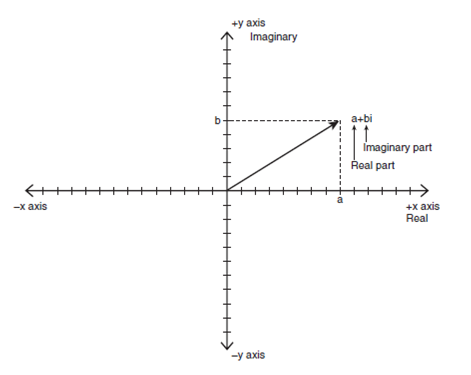
Complex Additive Identity
Also, the additive identity
(the complex number that, when added to any other complex number, is that
number) is (0+0*i), because:
(0+0*i) + (a+b*i) = (0+a +
(0+b)*i) = (a+b*i)
Complex Additive Inverse
The complex additive inverse
(the number that, when added to any other complex number, is the additive
identity (0 + 0*i)) is z* = (-a - b*i) for any complex number z = (a + b*i)
because:
(a + b*i) + (-a – b*i) =
(a-a) + (b-b)*i) = (0 + 0*i)
Complex Multiplication
Now for the fun part!
Multiplying complex numbers is actually very easy. Let’s do it, and pretend
like i is a variable, as we have before.
z1 = (a+b*i)
z2 = (c+d*i)
z1*z2 = (a+b*i) * (c+d*i)
= (a*c + a*d*i + b*c*i +
b*d*i2)
Noting that i2 = -1 and
collecting terms, we get
= (a*c + (a*d+b*c)*i + b*d*(-1))
Collecting terms once again,
we have
= ((a*c-b*d) + (a*d+b*c)*i)
Therefore, we see that the
real part equals (a*c - b*d), and the imaginary part equals (a*d + b*c). Let’s
do an example:
Example:
(1+2*i) * (-3 + 3*i) =
((-3-6) + (-6+3)*i) = (-9 - 3*i)
Complex Division
Division of complex numbers
can be accomplished using brute force. For example, we can compute the quotient
of two complex numbers z1/z2 in the following way:
z1 = (a+b*i)
z2 = (c+d*i)
(a+b*i)
z1/z2 = --------
(c+d*i)
If c = 0 or d = 0, then the
division is trivial, but if neither c nor d is equal to 0, then we are at a bit
of an impasse. To perform the division so that the result is in the form (a +
b*i) you must clear the denominator.
Hyper-Complex Numbers
Quaternions are nothing more
than hyper-complex numbers. The term hyper-complex can really mean anything
mathematically, but usually it means a complex number that has more than one
imaginary component. In our case, we are going to refer to hyper-complex
numbers with one real part and three imaginary parts—otherwise known as
quaternions. A quaternion can be written many ways:
The Form of a Quaternion
q = q0 + q1*i + q2*j + q3*k
or
q = q0 + qv, where qv = q1*i
+ q2*j + q3*k
i = <1,0,0>, j =
<0,1,0>, k = <0,0,1>, and <q0,q1,q2,q3> are all real numbers,
and i, j, and k are all imaginary numbers that form the vector basis of the
quaternion q. Moreover, q0 is real, and has no imaginary coefficient.
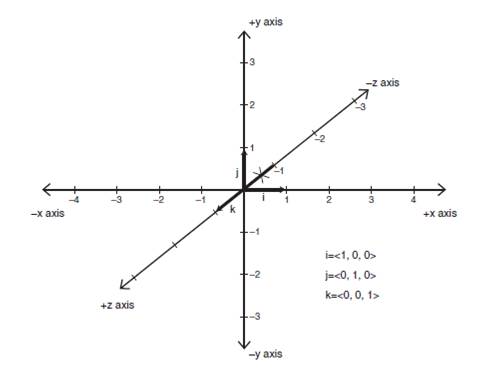
Also, the imaginary basis
<i,j,k> has the following properties. It can be
thought of as a 3D mutually perpendicular set of unit vectors in an imaginary
coordinate system that locates points in <i,j,k> space. But, the
interesting thing about <i,j,k> is the following
relationship:
The Quaternion Basis
Products i2 = j2 = k2 = -1 = i*j*k
MATH
Hold the imaginary basis i, j, k; thus, they are vectors,
and they are, but they can also be thought of as variables. They have a
dualistic nature, and sometimes it’s appropriate to think of them in their
vector form, and sometimes it’s not. Switch back and forth, especially when
using the i, j, or k alone or showing relationships
among them.
The “ =
i*j*k” part takes a little getting used to:
Given
i2 = j2 = k2
= -1 = i*j*k
therefore
i = j*k = -k*j
j = k*i = -i*k
k = i*j = -j*i
which intuitively seems right,
because the cross-product of any two perpendicular vectors in an orthonormal
basis should be perpendicular to the vectors themselves, or the third vector in
a 3D orthonormal basis. And if we invert the order of multiplication, we should
see an inversion or sign flip, and we do.
The conventions about
writing quaternions is using lowercase letters to represent them, but they also
break them up into a real and imaginary part, where they represent the
imaginary part as a vector like this:
q = q0 + qv
where
qv = q1*i + q2*j + q3*k
So q0 is the real part, and
qv is the imaginary part and is a vector <q1, q2, q3>. The fact that q,
the quaternion itself, is not bolded—it’s confusing because it’s a 4-tuple
itself. Use a notation in which quaternions are represented in lowercase bold,
AND the vector part is also in lowercase bold. Here’s an example:
a = -1 + 3*i + 4*j + 5*k
which in pure vector form is
a = <-1, 3, 4, 5>
or in real-vector form is
a = q0 + qv
where q0 = -1, and qv =
<3,4,5> = 3*i + 4*j + 5*j.
The point is that we are
going to use arrays obviously to represent quaternions in real life, and the
first number will always be the real part, and the remaining three numbers will
always be the imaginary coefficients of <i,j,k>.:
q = q0 + x*i + y*j + z*k
Or in another way:
q = q0 + <x,y,z> . <i,j,k>
Here, take advantage of the
vector property of <i,j,k>. That is, simply
referring to the real part as q0 and the imaginary part as qv = <x,y,z> when relating quaternions to 3D space. However, depending
on what going on, it might flip from one representation to another. Quaternions (or any hyper-complex number system) is that the
mathematics of addition, multiplication, inverses, and so on are all the same
as in standard complex number theory, but with more elements. We now have three
imaginary components rather than one, as with basic complex numbers or complex
numbers of “rank 1.” Here are some basic operations that might be needed to
perform on quaternions when doing calculations.
Quaternion Addition and
Subtraction
Addition or subtraction of
quaternions is accomplished by adding or subtracting the real part and the
imaginary part, just as with normal complex numbers.
Example:
q = q0 + qv
p = p0 + pv
q + p = (q0+p0) + (qv+pv)
Example:
q = 3 + 4*i + 5*j + 6*k =
<3,4,5,6> in vector form.
p = -5 + 2*i + 2*j – 3*k =
<-5,2,2,-3> in vector form.
q + p = (3+ -5) + ( (4+2)*i + (5+2)*j + (6+ -3)*k)
= -2 + 6*i + 7+j + 3*k
Writing of the imaginary
coefficients is <3,4,5,6> + <-5,2,2,-3> = <-2,6,7, 3>. However,
we have to be careful, because although it works for addition and subtraction,
for multiplication, recall that the last three components are complex. Keep the
quaternions in a form that at least keeps the real and imaginary parts
separate. Additive Inverse and Identity The additive
inverse of any quaternion q is the number that, when added to q, results in
zero. This is just –q:
Given:
q = q0 + qv
The additive inverse is just
-q = -q0 - qv
because
q - q
= (q0-q0)+ (qv- qv) = 0 + 0*i + 0*j + 0*j
The additive identity, or
“0” in quaternion math, must be
q = 0 + 0*i + 0*j + 0*k =
<0,0,0,0>.
Quaternion Multiplication
Because quaternions are
hypercomplex numbers based on real numbers with imaginary coefficients, we
should be able to just multiply them out, taking into consideration the
imaginary coefficients in the products and keeping track of them. Let’s just
try it and see what happens.
Given
p = p0 + p1*i + p2*j + p3*k
= p0 + pv
q = q0 + q1*i + q2*j + q3*k
= q0 + qv
then
p*q = (p0 + p1*i + p2*j + p3*k)
* (q0 + q1*i + q2*j + q3*k)
= p0*q0 +
p0*q1*i + p1*q2*j + p2*q3*k
+
p1*i*q0 + p1*i*q1*i +
p1*i*q2*j + p1*i*q3*k +
p2*j*q0 + p2*j*q1*i +
p2*j*q2*j + p2*j*q3*k +
p3*k*q0 + p3*k*q1*i +
p3*k*q2*j + p3*k*q3*k
The
structure to this product—maybe a crossproduct here and there, and a dot
product?
Use the equation to simplify the imaginary product terms:
= p0*q0 +
p0*q1*i + p1*q2*j + p2*q3*k
+
p1*q0*i + p1*q1*i2 +
p1*i*q2*j + p1*i*q3*k +
p2*j*q0 + p2*q1*j*i +
p2*q2*j2 + p2*q3*j*k +
p3*q0*k + p3*q1*k*i +
p3*q2*k*j + p3*q3*k2
Formula for Quaternion
Products Given
p = p0 + p1*i + p2*j + p3*k
= p0 + pv
q = q0 + q1*i + q2*j + q3*k
= q0 + qv
then
r = p*q = (p0*q0 – (pv . qv)) + (p0*qv + q0*pv + pv x qv)
= r0 + rv
Applications of Quaternions
Quaternions, by their 4D
nature, can handle standard vector angles and rotation matrices to perform
standard 3D rotations and manipulations, rotation of a vector and using
quaternions to interpolate camera orientations and so forth. Thus manipulating
a 3D camera with quaternions turns out to be more intuitive than using angles.
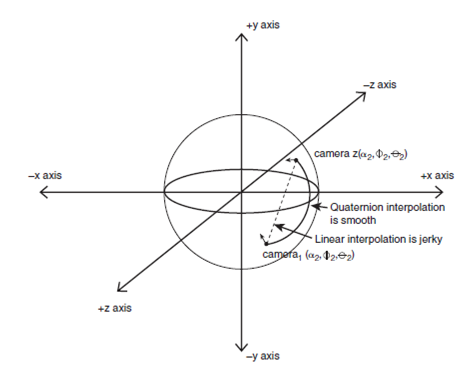
Quaternion Rotation
Right-handed system:
a. vq' = q* * vq * q,
clockwise rotation
b. vq ' = q * vq * q*,
counter-clockwise rotation
Left-handed system:
c. vq' = q * vq * q*,
clockwise rotation
d. vq ' = q* * vq * q,
counter-clockwise rotation
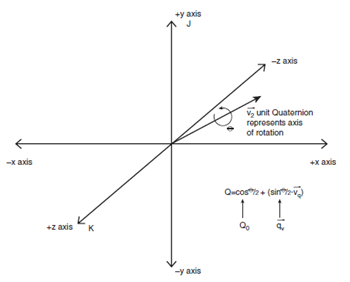
MATH
We can use q* in this
operator only for unit quaternions; otherwise, you must use the full inverse of
q.
So vq is a vector encoded in
a quaternion with q0 = 0, and q is a quaternion, but what exactly does q
represent? What’s its relationship to the x-y-z axis and vq? q defines both the axis of rotation and the angle θ to
rotate about the axis! Of course, the result vq' is technically a 4D vector or
a quaternion. However, the first component, q0, will always be zero, so we just
throw it away and think of the last three elements as just a vector in 3D
representing the original vector v after rotation. q = q0 + qv, the axis of
rotation is just the line defined by the vector part qv, and the angle of
rotation θ is encoded in q0 using the following transforms:
Conversion of Axis and Angle
to Quaternion
q = cos(θ/2)
+ sin(θ/2)*vq
Thus,
q0 = cos(θ/2)
and qv = sin(θ/2)* vq
qv must be a unit vector
itself, so that q remains a unit quaternion.
If you have Euler rotation
angles, you can then create a quaternion from the angles by generating one of
the products:
q-final =
qxθ*qyθ*qzθ
= qxθ*qzθ*qyθ
= qyθ*qxθ*qzθ
= qyθ*qzθ*qxθ
= qzθ*qxθ*qyθ
= qzθ*qyθ*qxθ
<-most common transform
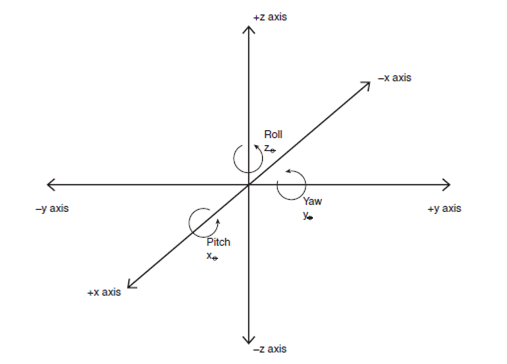
Yaw, pitch, and roll.
where xθ refers to the pitch
(angle parallel to the x-axis), yθ refers to the yaw (angle parallel to
the y-axis), and zθ refers to the roll (angle parallel to the z-axis.
After you have the order of transforms, you can plug in the following formulas
for the quaternions qxθ, qyθ, qzθ and perform the multiplication
to arrive at qfinal.
Euler Angles to Quaternion:
qxθ = cos(xθ/2) +
sin(xθ/2)*i + 0*j + 0*k
q0 = cos(xθ/2),
qv = <sin(xθ/2), 0, 0>
qyθ = cos(yθ/2) + 0*i+
sin(yθ/2)*j + 0*k
q0 = cos(yθ/2),
qv = <0, sin(yθ/2), 0>
qzθ = cos(zθ/2) + 0*i +
0*j + sin(zθ/2)*k
q0 = cos(zθ/2),
qv = <0,0,sin(zθ/2)>
To rotate a vector v using
the Euler form do the following for the
example of roll, yaw, and pitch:
vq’(0,x’,y’,z’)
=(qzθ*qyθ*qxθ )* vq * (qzθ*qyθ*qxθ)*
where vq = <0,x,y,z>, the
initial vector or point we want to rotate cast into quaternion form. Of course,
you only need to compute the product in parentheses once. And because each of
the factors qxθ, qyθ, qzθ is of the form below:
q(i,j,k) = cos(θ/2) +
sin(θ/2)*(i,j,k)
The product of terms of this
form have a lot of cancellations—thus the product
qzθ*qyθ*qxθ, ends up
looking like this:
q0 = cos(zθ/2)*cos(yθ/2)*cos(xθ/2)
+ sin(zθ/2)*sin(yθ/2)*sin(xθ/2)
q1 = cos(zθ/2)*cos(yθ/2)*sin(xθ/2)
- sin(zθ/2)*sin(yθ/2)*cos(xθ/2)
q2 = cos(zθ/2)*sin(yθ/2)*cos(xθ/2)
+ sin(zθ/2)*cos(yθ/2)*sin(xθ/2)
q3 = sin(zθ/2)*cos(yθ/2)*cos(xθ/2)
- cos(zθ/2)*sin(yθ/2)*sin(xθ/2)
Basic Calculus
Physics is why calculus was
invented. It is needed to calculate collision detection with real math and real
models. Calculus is a form of mathematics invented independently by both Sir
Isaac Newton and Baron Gottfried
Wilhelm
Leibniz in the 17th century. “The Calculus” (as it’s referred to) was
invented as a tool to help solve problems in motion, change, and dynamic
systems that standard static algebra of the time couldn’t handle. Thus,
calculus is the mathematics of change, or systems in flux.
How to perform a
mathematical operation that results in infinity? For example the following
quotient:
1
q = ----
y
What happens if y becomes
very small, is the question that calculus answers.
1/1 = 1, 1/.1 = 10, 1/.01 =
100, 1/.001 = 1000,…
As y gets smaller and
smaller, the quotient of 1/y gets larger and larger. Therfore
the numerator 100,000,000,000. The point is that as the denominator gets
very small, the quotient gets larger and larger without boundary. At some
point, the denominator will become zero, but what will the quotient become? The
answer is plus infinity.
x/0 = +∞, +infinity and
x
--- = 0
∞
Which makes sense, because
if you look at the following sequence, you can see it: 1/1 = 1, 1/10 = .1,
1/100 = .01, 1/1000 = .001, …
As the denominator gets
larger and larger, the quotient gets smaller and smaller, and inthe e nd the
result will be zero. The last question you might ask is what happens if both
the numerator and the denominator go to infinity? Well, it depends on which one
gets there faster. Let’s think about it with common sense. Take a look at this:
500*x
y = ----------
x*x
The question is, what happens when x approaches infinity? Well, in the
numerator we have 500*x, and in the denominator we have x*x. Here’s a short run
of the numerator and denominator for x ∈ (0,1,2,3,4,5,6,7,8,9,10):
A run of numbers in the
Quotient 500*x/x2
x Numerator 500*x) Denominator(x*x)
Quotient
0 0 0 Indeterminate
1 500 1 500
2 1000 4 250
3 1500 9 166.66
4 2000 16 125
5 2500 25 100
6 3000 36 83.33
7 3500 49 71.42
8 4000 64 62.5
9 4500 81 55.55
10 5000 100 50
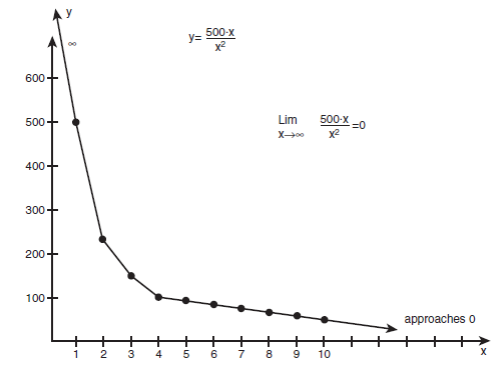
A graph of
the quotient 500*x/x2. Also, take a look at the graph. Although it seems that the
numerator is moving very quickly, the denominator is quickly catching up, and
thus the quotient is getting smaller and smaller. In fact, the end result will
be zero. So does common sense seem right? Well, at first glance, if you didn’t
run the sequence, you might say that the numerator is much larger, and it is
for small x. But as x gets large, the x*x is much larger than 500*x, so the end
result is that the rate of increase of the denominator is greater than the
numerator. Hence, the result will be zero in this case.
500*x
y = ------- = 500/x
x*x
As shown x approaches
infinity, anything divided by x approaches zero. This property will be
discussed in the section devoted limits.
Limits
A limit is a mathematical
statement that describes has a changing variable that approaches a fixed
constant. This is the very point of calculus—being able to write down in a
consistent manner changing mathematical concepts. In any case, here’s the
general form of a limit statement:
Lim f(x) = L
x->a
This is read “The limit of
f(x) as x approaches a is equal to L.” To compute a
limit, you let x approach the limiting value and read off the result.
Example 1: Simple limit
Lim 2*x =
?
x->3
As x approaches 3, nothing
weird happens with f(x). Thus we can simply replace x with 3,
and the limit is equal to
Lim 2*x = 2*(3) = 6
x->3
Example 2: Indeterminate
limit
Lim x*x/3*x
x->0
If we let x approach 0, then
we get
Lim 0*0/3*0 = ? x->0
which is indeterminate (0/0 is
not computable). We need to see whether we can simplify the limit first, so we
can get a better grasp on what’s happening:
Lim x*x/3*x
x->0
Canceling out the x terms in
numerator and denominator gives us
Lim x/3 = 0
x->0
which clearly equals zero,
because 0/3 = 0.
Example 3: Infinite limit
Lim 1/(5*x*x
+ 2*x) = ?
x->∞
In this case, the bottom
line is that as x gets larger and approaches infinity, (5*x*x + 2*x) gets
larger and approaches infinity even faster. Thus the quotient goes to
1/∞, which is equal to zero.
Summation and Finite Series
Many times when solving
problems that are iterative or recursive in nature, we see sequences of numbers
or terms that have patterns. For example, take a look at the following
mathematical sequence or summation:
1+2+3+4+..n
The way to write it is to
use sigma notation (the Σ symbol). The preceding sequence has a lower
limit (1), an upper limit (n), and a rule. In this case, the rule is at each
step simply add the next number in the sequence.
b
Σ f(n)
n = a
where a <= b (but not
necessarily), a is called the “lower limit,” and b is called the “upper limit.”
If n was equal to 1000, how long do you think it would take to add the numbers
1 to 1,000 up? The formula for this, by the great mathematician Karl Gauss:
The Sum of the First n
Integers
n
Σ k = 1+2+3+…+n =
n*(n+1)/2
k = 1
Plugging in 1000, we get
1000*(1000+1)/2 = 500500
The Sum of the First n
Squares
n
Σ k^2 =
1^2+2^2+3^2+…+n^2 = n*(n+1)*(2*n+1)/6
k = 1
The Sum of the First n Cubes
n
Σ k3 =
1^3+2^3+3^3+…+n^3 = (n*(n+1)/2)2
k = 1
Question:
n
Σ 3*k = ?
k = 1
The first thing we do is
write out a few terms to see the pattern, and find out whether we can
manipulate it into one of our formulas and solve it.
n
Σ 3*k = 3*1 + 3*2 + 3*3
+…+3*n
k = 1
Looks like 3 is always
there, so let’s factor it out of the sigma sign like this:
n
Σ 3*k = 3*1 + 3*2 + 3*3
+…+3*n
k = 1
n
= 3*Σ k = 1 + 2 + 3
+…+n
k = 1
= 3*n*(n+1)/2
Or in general, for any
scalar a:
n
Σ a*k = a*n*(n+1)/2
k = 1
Infinite Series
Finite sums are things that
are very tangible—they end somewhere. But there are mathematical sequences that
go on forever, but aren’t infinite! How can something go on forever, but not be
infinite?
0 + 0 + 0
+ …
An infinite sum of zeros is
definitely still zero. This is the theme of the next section. There are many
times when a complex system can run forever, but its height, energy, level, and
so on are changing each time.
Domain: 0 1 2 3 … n
↓ ↓ ↓ ↓ ↓
Range: 0 5 10 15 5*n
In this case, the domain is
the positive integers 0, 1, 2 … and the range is also the positive integers.
The rule is multiply the integer by 5. The question is,
what is the sum of this infinite series? Common sense tells us that the series
keeps getting larger and larger, and thus must grow unbounded, and hence the
sum is infinity. However, there are other series that do converge to a finite
number. For example, series of the following form can converge to a finite
value, if the values of a and r satisfy certain
constraints:
∞
Σ a*r(n-1)
= a + a*r + a*r2 + a*r3 +…+ a*rn+ …
n=1
where a and r are real numbers,
and a ≠ 0. Infinite series of this kind are called geometric series.
Here’s an example:
a = 5, r = 1/2
∞
Σ a*r(n-1)
= a + a*r + a*r2 + a*r3 +…+ a*rn+ …
n = 1
= 5 + 5*1/2 + 5*(1/2)2 +
5*(1/2)3 + …
= 5 + 5/2 + 5/4 + 5/8 + …
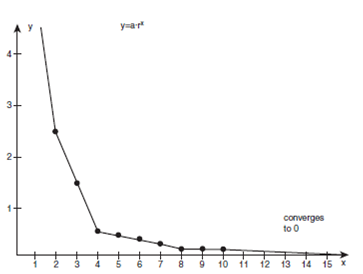
The series is getting
smaller and smaller, and this is confirmed by the plot of points. In fact, when
n reaches infinity, the terms will approach zero.
Sum of a General Geometric
Series
∞
Σ a*r(n-1)
= a + a*r + a*r2 + a*r3 +…+ a*rn+…
n = 1
the sum = a/(1-r), for |r|<1
It tells us how to compute
the sum of an infinite collection of expressions in a closed form—math. Using
theformula on our series from the previous example with a = 5, and r = 1/2, |r|
is less than 1, the sum is a/(1-r) = 5/(1/2) = 10.
Derivatives
The derivative of a function
is the instantaneous rate of change of that function. For example, suppose you
have an object in a game, and its position is described by the following
formula, as shown:
x = x0 + vel*t
This obviously means that
the position x at any time is x0 plus the factor vel*t, where t could be time,
or some artificial variable, like the current frame. Given the formula for x,
what is the instantaneous rate of change of x? The answer to this is in the
definition of x, because with each increment of t, x will change by vel*dt, or velocity*1. Thus, the instantaneous rate of change is
the rate factor vel itself. If we differentiate x with respect to t, the result
is the rate of change of x with respect to t. The derivative of the position is
the velocity.
The derivative looks like:
d/dt * x(t)
which means take the derivative
of x with respect to t.
d/dt * x(t) = vel
Definition of Derivative
A curve or function of x,
f(x) also, labeled a, which has the value x0, and b, which has the value x0+h
(h is just a number), and between the two points you see a tangent line with a
slope. The slope of this tangent line is shown in
Definition of the Tangent
Line
dy f(x0+h) – f(x0)
slope = --- ----------------
dx h
This slope is only an
average or approximation, but what if we want the slope exactly at x0? We can
just make h smaller and smaller to find this. We want to make it infinitely
small (zero), so that we are dead on x0. Alas, there’s a problem with this!
Look at this limit:
lim f(x0+h) – f(x0)
h->0 ---------------
h
As h approaches zero, this
limit looks like it might approach infinity, and we are fragged! However, this
is the definition of the derivative:
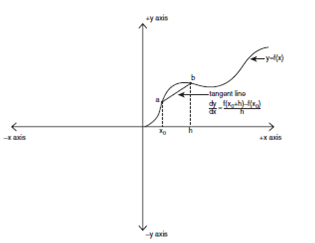
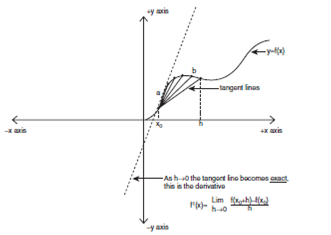
f’(x) = lim f(x0+h) – f(x0)
h->0 ---------------
h
The notation f'(x), or “f
primed," means “the derivative of f with respect to x,” so that’s just
notation. Similarly, f’’(x) would mean “the second derivative of f with respect
to x,” or the derivative of the derivative. In general, these all mean the same
thing:
1. f'(x)—The
derivative of f with respect to x. Both the function and the variable are
mentioned.
2. (d/dx)*f(x)—The derivative with respect to x of the function. Emphasizes that differentiation is an operator.
3. df/dx—Very similar to
number 1, but in another format. Emphasizes both the function
f and the variable to differentiate. If the limit exists then it is the
derivative.
Derivatives of Simple
Polynomials
Computing the derivatives of
polynomials is the simplest, so let’s start here. First, the derivative of the
sum of terms in a polynomial is simply the sum of each of the derivatives:
f(x) = f1(x) + f2(x) + … +
fn(x)
f’(x) = f1’(x) + f2’(x) + …
fn’(x)
To compute the derivative of
any polynomial term, here’s what you do:
Let f(x) = a*xn
f’(x) = n*a*x(n-1)
Example 1:
f(x) = 5*x3
f’(x) = 3*5*x(3-1) = 15*x2
Example 2:
f(x) = 3*x2 + 2*x + 5
or, writing out all the terms,
df/dx = 3*x2 + 2*x1 + 5*x0
df/dx = 2*3*x(2-1) + 1*2*x(1-1) +
0*5*x(0-1)
= 6*x1 + 2*x0 + 0
= 6*x + 2*1 = 6*x+2
NOTE
Note that the derivative of
a constant is zero. Many times, one notation is more convenient than another,
as you will see. Before moving on, let’s look at a couple of general rules for
computing derivatives.
Derivatives of Products: The
Product Rule
When you compute the
derivative by taking each expression separately, rather than computing each one
is called the product rule. It looks like this:
Given u(x) and v(x) are
functions of x, (d/dx)*(u * v) = u*(dv/dx) + v*(du/dx)
which reads “The derivative of
the product u multiplied by v is u multiplied by the derivative of v with
respect to x added to v multiplied by the derivative of u with respect to x.”
Example:
f(x) = (3*x2 + 3) * (5*x)
Let
u(x) = (3*x2 + 3), v(x) =
(5*x)
then
f’(x) = u(x)*v’(x) +
v(x)*u’(x)
= (3*x2 + 3)*5 + (5*x)*(6*x)
Derivatives of Quotients:
The Quotient Rule
Computing the derivative of
a quotient can be accomplished using the product rule and inverses, but to make
life easier, we usually just use what’s called the quotient rule and leave the
problem in its original form. Here it is again, in a slightly modified
notation:
Given u(x) and v(x) are
functions of x,
(d/dx)
* (u/v) = [ v*(du/dx) – u*(dv/dx) ]
---------------------------------
v2
which reads “The derivative of
the quotient u divided by v is equal to v multiplied by the derivative of u
with respect to x minus u multiplied by the derivative of v with respect to x,
quantity divided by v squared.”
Example:
Given
4*x3 – 3
f(x) = ---------
-3*x2
Let
u(x) = (4*x3 – 3), v(x) =
(-3*x2)
then
[v(x)*u’(x) – u(x)*v’(x)]
f’(x) =
-------------------------
v(x)2
= [(-3*x2)*(12*x2) - (4*x3 –
3)*(-6*x)]
----------------------------------------
(-3*x2)2
Again, note the change of
notation. Also, we could simplify this if we wanted to.
The Chain Rule
Take a look at the following
function:
f(x) = sqrt(x2+1) = (x2+1)1/2
This problem could be solved by finding the
derivative of f(x) directly (if we can), or we could think of f(x) as a
composition of two or more functions. Composition means nothing more than one
function is the parameter to another. In this case, if we let g(x) = (x2+1),
and f(x) = sqrt(x), we can write this:
Given
f(x) = sqrt(x) = (x)1/2
and
g(x) = (x2+1)
If we replace the “x” in the
definition of f(x) with the function for g(x), we have composed g with f, or
mathematically:
f(g(x)) = (f • g)(x) =
(x2+1)1/2
NOTE
Note that the notation f(g(x)) and (f • g)(x) are equivalent. As another example,
let f(x) = sin x, and g(x) = (2*x+3), then f composed with g is
(f • g)(x) = sin (2*x+3)
The chain rule states that
you can compute the derivative of a function by first computing the derivative
of the composition, and then multiplying that by the derivative of the inside
function. Then, if the inside function needs to be further simplified as more
compositions, you continue the process.
Mathematically, the chain
rule can be stated as the following:
(d/dx)f(g(x))
= f’(g(x)) * g’(x)
Let’s take another look at
the first example with f(x) =(x)1/2, g(x) = (x2+1),
and apply the rule.
f(g(x)) = (x2+1)1/2
f’(g(x)) = f’(g(x)) * g’(x)
= (d/dx)(g(x)1/2)
* (d/dx) g(x)
= ?*((x2+1)-1/2 * (2*x)
= x/(x2+1)1/2
Derivatives of Trigonometric
Functions
sin x cos x
cos x -sin x
tan x sec2 x
cot x -csc2 x
sec x = 1/cos x sec x * tan x
csc x = 1/sin x -csc x * cot x
f(x) = cos2 x
Product rule with
f(x) = cos(x) * cos(x)
Let
u = cos(x), let v = cos(x)
then
f’(x) = u*(dv/dx) + v*(du/dx)
= cos(x) * sin(x) + cos(x) *
sin(x)
= 2*cos(x) * sin(x)
Let u = a, v =
transcendental(x), where the trig function could be anything. Then we have:
f’(x) = u*(dv/dx) + (du/dx)*v
= a * transcendental’(x) + 0
= a * transcendental’(x)
Note that the derivative of
u is 0, so the product of the second term is also 0, thus leaving us with the
original constant multiplied by the derivative of the transcendental function.
Here’s an example:
Given
f(x) = 3*cos(x)
f’(x) = -3*sin(x)
Finally, let’s look at
problems of this form:
f(x) = a*cos(b*x+c),
a*sin(b*x+c), a*tan(b*x+c), etc.
There’s a multiplier in the
parameter part, along with a constant that models the time multiplier and a
shift. This is just a composition, so use the chain rule here, letting the
inside function be g(x) and the outside function be f(x). Let’s try figuring
out
a*sin(b*x), as all the others
are identical.
Given
f(x) = a*sin(b*x+c)
f’(x) = a*[(d/dx)sin(b*x+c)]
Thus, our problem really
boils down to computing this:
f(x) = sin(b*x+c)
The chain rule results:
Let
g(x) = (b*x+c)
f(x) = sin(x)
then
f(g(x)) = sin (b*x+c)
f’(g(x)) = f’(g(x)) * g’(x)
= (d/dx)sin(g(x))
* (d/dx)(b*x+c)
= cos (b*x+c) * b
Further.
f(x) = a*sin(b*x+c),
f’(x) = a*[(d/dx)sin(b*x+c)]).
f(x) = a*sin(b*x)
f’(x) = a*(cos(b*x+c)* b)
= a*b*cos(b*x+c)
Integrals
Integration is the opposite
of differentiation— or antiderivative. If you were to
differentiate f(x) to arrive at f'(x), what would you do to f'(x) to get back
to the original f(x)? This process is called integration. The first and
purest way to look at the antiderivative is with its definition:
Given a function
f(x) and its derivative f'(x),
the antiderivative F(x) is a function such that if you differentiate it, you
get f(x):
F’(x) = f(x)
If you have a function f(x),
and another function capital F(x) that you want to be the antiderivative of
f(x), the derivative of F'(x) will equal the original function f(x). That’s not
that useful, so let’s try an example like f(x) = 2*x. Now, the antiderivative
of (2*x) is a function F(x), such that when the derivative of it, the result
would be (2*x). F’(x) = 2*x
What function when the
derivative is taken, equals (2*x)?
The answer is x2 because
(d/dx)x2 = 2*x(2-1) = 2*x.
The
antiderivative of any term of the form a*xn. We just reverse the process
of differentiation, which states to multiply by the exponent and then decrease
the exponent. Reversing that, we get the process for integration, which must be
to divide by the exponent and then add one to the exponent. Mathematically, the
antiderivative of a*xn is a*xn = (a/(n+1))x*(n+1) + c.
Definition of Antiderivative
Integration is the process
of computing the antiderivative of a function, and is written using the ∫
symbol, like this:
∫ f(x)dx
= F(x) + c
f(x) is the function we want
to find the antiderivative of, F(x) is the antiderivative, and c is the
constant of integration. The function g(x) = 2*x+1 differentiated is this:
g(x) = 2*x1+1
g’(x) = 1*2*x(1-1) + 0
= 2
The result is 2, which was
just an example to show you that constants disappear when you differentiate.
Now if we wanted to compute the antiderivative of that 2, knowing that we
should end up back at (2*x+1). Using our antiderivative rule relating functions
of the form a*xn to the antiderivative (a/(n+1))x*(n+1):
F’(x) = 2*x0
F(x) = (2/1)*x(0+1) = 2*x
A functions derivative and
then used it as the new starting point and found its antiderivative thinking we
would end up in the same place. You lost some information—the constant 1.0 in
this case. This leads us back to the definition of an integral:
∫ f(x)dx
= F(x) + c
The c takes this factor into
consideration; that is, we know we could potentially lose information when we
integrate to find the antiderivative. Only in cases where c = 0 can we forget
about it; otherwise, we must keep this in mind. Thus in the example, we just
computed that we need to add an arbitrary constant to the result, giving us
(2*x+c).
Integration is the opposite
of differentiation, and the result is called the antiderivative. We know that
the antiderivative of functions of the form a*xn is [(a/(n+1))x*(n+1)
+ c], where c is the constant of integration, and may be non-zero. In a moment
we will talk about integrals of trig functions, but now I want to give you
something more tangible to think about in relation to integration.
A Geometric Interpretation
of Integration
Differentiation is like
computing the instantaneous rate of change or slope of a function. That is,
when you differentiate a function f(x), you wind up with another function f'(x)
that is the slope of f(x) for any x. Integration has a similar geometric
interpretation in the opposite sense. Take a look at
A common parabola function
f(x) = x2 in the interval of [0,5]. Additionally, I
have shaded in the area under the curve. Interestingly enough, integration
computes the area under the curve! Let’s test that out. Given the initial
function f(x) = x2, let’s integrate it using the formula:
∫ f(x)dx
= F(x) + c
and
f(x) = x2
∫ x2dx = F(x) + c
Using our antiderivative
formula (a/(n+1))x*(n+1), we get
∫ x2dx = x3/3 + c
Now, what’s c? That’s where
the interval comes into play ([0,5]). We need this to
lock into and compute c. The integrals is called indefinite integrals they
compute a family of functions for the antiderivative because c is unknown, but
definite integrals compute the exact value for c, and hence a single
antiderivative. The definite integral a little differently.
b
∫ f(x)dx
a
where [a,b] are the limits of
integration: Here it is again.
Step 1: Compute the
integral.
5
∫ x2dx = [x3/3 + c]
0
Step 2: Plug in the limits
of integration and evaluate the integral at the upper limit and lower limit and
subtract.
5
= [x3/3] = [(5)3/3 - (0)3/3]
0
= [125/3 – 0]
= 41.66
Compute the integral as
usual, then after you have the general form of the integral, you plug the upper
limit of integration into the result to arrive at a number, then do the same
with the lower limit, and then subtract. This gives you an exact answer
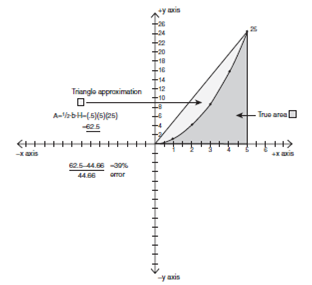
A triangular approximation
of the area under the curve f(x) = x2. In this case, the answer should be the
area under the curve f(x) = x2 in the interval of [0,5].
We get 41.66 roughly; let’s see whether that’s in the ballpark. Because there
are no formulas for computing areas under curves, we can use a triangular
approximation. The height of the triangle is 25 and the width is 5, so the area
is
A = ?*width*height
= ?*5*25 = 62.5
which tells us that we are in the
ballpark, because the area under the curve is of course less. In fact, the area
is exactly 41.66.
Integration Formulas
Okay, so now we have
mathematical definition for integral, a geometric interpretation, and we know
how to integrate both indefinite and definite integrals. Now let’s take a
lookat some formulas for integration.
Integration Formulas
Integral Antiderivative
∫ a*un
du (a/n+1)*u(n+1) + c
∫ sin u du -cos u + c
∫ cos
u du sin u + c
∫ sec2
u du tan u +c
∫ csc2
u du -cot u + c
∫ sec
u * tan u du sec u + c
∫ csc
u * cot u du -csc u + c
Summing is exactly what
integration does. It sums a function from one point to
another. That’s a very useful
operation, and absolutely necessary when calculating physics models. Because
most of the time, you will have a model:
Position: x(t)
= x0 + v*t
Velocity: v(t)
= v0 + a*t
where the acceleration a is
constant. The time derivative of the position x(t) is
equal the velocity v(t), or (dx/dt)x(t) = v(t), or put yet another way:
x’(t) = v(t)
That means if I have the
formula for v(t), its antiderivative must be equal to
x(t).
Mathematically, we have
x’(t) = v(t)
So, integrating both sides:
∫ x’(t)
dt = ∫ v(t) dt
The left-hand side is just x(t), because the antiderivative of the derivative of a
function
f'(x) must be f(x) again.
Thus we have:
x(t) = ∫ v(t) dt
And we already know the form
of v(t) = v0+a*t; plugging it into the indefinite integral,
we get
x(t) = ∫ v0+a*t dt =
[v0*t + 1⁄2*a*t2 + c]
And now all we need is c.
But, if we use the initial conditions t = 0, x = x0, and v = v0, we get
[0 + 0 + c] = x0
therefore c = x0.
Putting it all together, we
get the final formula for motion as a function of time, and the initial
position and velocity with constant acceleration:
x(t) = ∫ v0+a*t dt =
[v0*t + 1⁄2*a*t2 + x0]
To integrate the velocity
function to find the position is exactly what physics modeling is all about.
You run the model, compute collisions and forces, and then you need to
integrate numerically to find the new position of all the objects in the game.
…and that is the foundation
of math. “Do you think that that’s air you are breathing.”
Morpheous, the Matrix.
The brain will solve any problem if
presented to it difference in quantity change and/or difference of rate of
difference of quantity in the form of a solution set of generalization(s). The
generalization is a landscape. The quality of landscapes have
been described in general in the previous chapter and is sufficient for all
topic in this text and beyond. The landscape is renormalized in RC->G
process progressively or regressively in respect to quantity or rate of
quantity for any property the brain receives. You have to format questions
correctly understanding how the brain works to get answers to questions. There
is a caveat to this fact. The brain is like everything else a quantum machine.
The emergent mind, which is a perception, has limitations. The inputs the brain
receives originate from local and non-local sources of the field. The mind has
been studied and experimentally proven perception limitations in the form of
the emergent mind's:
Process speed
- Sharp
drop off of accuracy when and increase of on objects to focus on increases
- Learned
and hardwired predispositions like politics, faith, experience, etc.
- Echoes
in genetics, heightened or underdeveloped local and non-local noise
The brain will perform its conception
operation on garbage and information. Its error correction is perception and
bad perception will corrupt processed data or perception of any kind. Only
efficient perception will permit error correction on conception. Efficient
CRP->G is flow of conception, persistent resilient reception and landscape
constructing perception. The brain field paradigm is a continuum and therefore
inseparable. Conception is modifiable by perception in the form of the effort
of learning.
What is Electricity?

All matter affect electrical properties due to the fundamental
particle, the electron. Renowned scientist Erwin Schrödinger, 1926 gave the
most accurate mathematical description of the behavior of electrons. The
eponymously named Schrodinger equation is a statistical probability average,
which predicts the most likely location of an electron, which is naturally
observed in a region near the nuclei of atoms and as free particles, which
occupy discrete probability amplitude, most accurately behaving as standing
wave.
![]()
where:
![]() is the square root of negative one
is the square root of negative one
![]() is the reduced Planck's constant
is the reduced Planck's constant
![]() is time
is time
![]() is a place in space
is a place in space
![]() is the wave function
is the wave function
![]() is the Hamiltonian energy operator:
is the Hamiltonian energy operator:
The basic principle is
that the wave function Ψ permeates all of space and evolves according to
Schrodinger’s equation. The function Ψ encodes the probability of finding
the electron particle within any given region (as well as probabilities for its
momentum, energy and so on). This theory can predict the outcomes of
experimental observation with impressive accuracy.
Computers are tools which are tasked with
converting the known world into an electronic system to perform meaningful
operations on input. Math is a human language construct which communicates the
world as we understand it. The world or field is a substrate which expresses a
system of operations very similar to a computer.
Scale or sizing a system is a fascinating
view of the field as we delve into the understanding of the world. Here, think
of world as the mind’s conception of the field. The field is and the conception
of it is our connection. When you scale an understanding of electronic
properties, it ranges currently from quantum electrodynamics theory of
Schrödinger to Maxwell electronic functions that describe attraction and
repulsion of these fundamental buggers, the electron.
The Maxwell Equations formalize our
understanding of the behavior of electrons in the field like this.
Equation 1: Gauss' Law Ñ ·
D = ρν
Equation 2: Gauss' Magnetism Law Ñ
·
B = 0
Equation 3: Faraday's Law Ñ ·
E = - ∂B / ∂t
Equation 4: Ampere's Law Ñ X H = - ∂D / ∂t + J
Related Equations
Continuity Equation
The Wave Equation Math Ñ X Ñ
X H = Ñ X (Ñ
X H)- Ñ
ˆ 2 H
The Curl Ñ X
Divergence Ñ ·
Partial Derivative g(x,y,z)
= ∂ƒ(x,y,z)/∂x
Vector
Equation
They
govern themseles in nature. The way the electric and magnetic field distribute
themselves what kind of physical phenomina give rise to them.
1. Gausses Law - Charges of the same sign
repel each other. The divergence symbol express that fields
are positioned around a point. The D represents the charge and it equals
ρν
- Electric Charge Density
ρν - The greek symbol pho (electric charge) denotes
electric charge, and the subscript V indicates it is the volume charge density. This density is measured in columbs. For a
small point charge an eminating field line is negative and flows inward or if
it is positive the charge field eminates outward.
2. Gausses Law of Magnetism- The
divergence of the magnetic fiels is zero. There is no isolated magnetice
charge. You cannot find a magnetic monpole. You will never fiend a magnetic
pole or field eminating outward from a point electric partilcle, according to
this law. Which is a bit speculative with the recent discovery of monopoles
magnetic particles, but that’s another story.
3.
Faradey law - Dell cross means curl. Describe how the field wraps around the
flow of electric fields. Here the divergencence is the curl and is eqaul to the
rate of change of the magnetic field in repect to time. This magneticfield was
originally discovered by measuring the magnetic field through an electric
circuit. The curl of the electric field is related to the time rate of change
of the magnetic field.
4. Ampere law - The curl of the magnetic field in
respect to the change of the electric field in repect of time plus the electric
current density. Current flow in a wire and magnetism wraps around it. The
displacement current density occurs at the gaps of a capacitor. Current crosses
a gap because of the magnetic presence at the end of a conductor. Permeability µ
- The permittivity of a material relates the Electric Flux Density to the
Electric Field. Similarly, materials can be classified by their permeability,
which relates the Magnetic Flux Density to the Magnetic Field. The permeability
is most often denoted by the Greek symbol mu (permeability symbol). Don’t
confuse permeability with conductivity σ. Electrical conductivity is a
measure of how easily electric current can flow through a given material. That
is, for a given electric field in a material, a higher conductivity material
will produce more current flow than a low conductivity material.
Thus the wave equation. The wave going in
the z direction
is equal to the change in the rate of change. Light propagation without a
conduit like fiber optic wire occurs because the wave nature of light that is
electromagnetism curling around electric field in relation to time change which
continues until the frequency of light becomes longer and longer and less
detectible to measure or see.
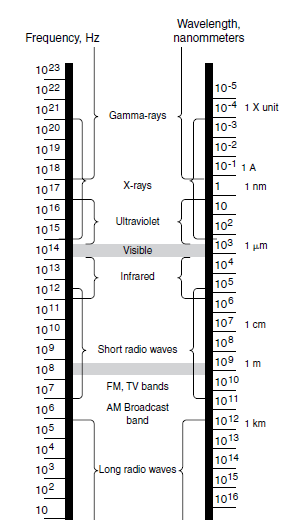
Common colors
400 to 450 nm Violet
450 to 500 nm Blue
500 to 550 nm Green
550 to 600 nm Yellow
600 to 650 nm Orange
650 to 700 nm Red
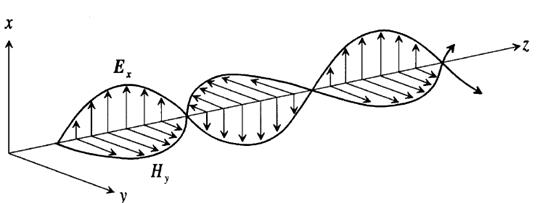
The manipulation of electrons is the basis
of biological and electronic computation. Electron voltage, current, and
Resistance are synonymous with more familiar natural phenomena like water
pressure, flow and impedance in a stream. Electronic components such as diodes
and transistors form the damns and rivers of the integrated circuit. These
circuits are combined to create switches, which are engineered to create logic
gates. Using Boolean mathematics, these logic gates are arranged to perform arithmetic
operations. The surface of an IC chip is micro cities, housing and controlling
the traffic of the electron community. Layers of neuron paths in brains and
hardwired strategic gates make computation a reality.
Electrons may be released from their atoms
by various means. Some atoms of certain elements release their electrons more
readily than atoms of other elements. If an atom has an equal number of
Electrons and protons, it is said to be in balance. If an atom has given up
some of its electrons, the atom will then have a positive Charge and the matter
that received the electrons from the atom
will
be negatively charged. Some external force must be used to transfer the
electrons.
Contact between the two surfaces results
in the one being robbed of some of its negative electrons, thereby leaving it
positively charged, while the other
Surface acquires a surplus of negative
electrons and is thereby negatively
charged.
It is important to note that this surplus of negative electrons doesn’t come
from the atomic structure of the fur itself. It is found that, in addition to
the electrons involved in the structure of materials, there are also vast
numbers of electrons “at large.” It is from this source that the negatively
charged surface draws its negative charge of electrons.
When a body acquires an electrical charge
as, for example, the hard rubber rod or the glass rod previously described, it
is customary to say that the lines of force emanate from the surface of the
electrified body. By definition, a line of electrical force is an imaginary
line in space along which electrical force acts. The space occupied by these
lines in the immediate vicinity of an electrified body is called an
electrostatic field of force or an electrostatic field.
Electric Current
We learned earlier that static electricity
refers to electrical charges that are stationary—that is to say, a surplus of
electrons, or the lack of same, that stay in one place, not in motion.
Electrons in motion constitute an electric current. Thus, if electrical
pressure from a battery, generator, or other source is applied to an electrical
conductor, such as a copper wire, and the circuit is closed, electrons will be
moved along the wire from negative to positive. These electrons pass from atom
to atom and produce current. The electrons that move are free electrons.
There are basically three forms of
electrical current, namely (1) direct current (DC), (2) pulsating direct
current (pulsating DC), and (3) alternating current (AC).
DC motor generates current flowing
steadily in the direction represented by the arrows.
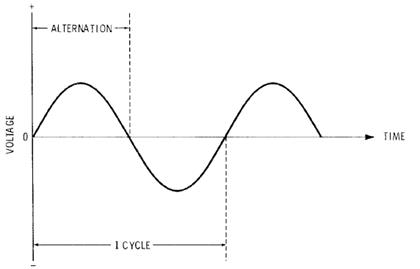
Representation of one alternation and one
cycle, which consists of two alternations.
Insulators and Conductors
An insulator opposes the flow of
electricity through it, whereas a
conductor
permits the flow of electricity through it. It is recognized
that
there is no perfect insulator.
Definitions
A number of definitions will be given at
this point in the course. There will be others given as we progress. The reason
for giving these here is that we may use electrical terminology as we progress
and keep the explanations to a minimum. Insulation: A material that by virtue
of its structure opposes the free flow of current through it. Commonly used
insulating materials are asbestos, ceramics, glass, mica, plastics, porcelain,
rubber, and paper.
Conductor: A material that allows the free
flow or passage of an electric current through its structure; generally, any
wire, cable, or bus suitable for carrying electrical current.
Ampere (A): The unit of intensity of
electrical current (I); rate of flow of electric charge. One ampere will
deposit silver in an electrolytic cell at the rate of 0.001118 gram per second.
Ohm (Ω): The unit of resistance (R)
to an electrical current; a column of mercury 106.3 cm long and having a mass
of 14.4521 grams (approximately) with a 1 square millimeter cross section at 0°
Celsius has a resistance of 1 ohm.
Units and Definitions 15
Volt (V): The unit of electrical pressure
(E); electromotive force (emf); potential difference. The amount of electrical
pressure required to force 1 ampere through 1 ohm of resistance.
Coulomb (C): The quantity of charge that
passes any point in an electric circuit in 1 second when 1 ampere of current is
present.
Watt (W): The electrical unit of energy;
rate of doing work (P). The product of the applied volts and the current in the
circuit: 1 ampere
1 volt [1]
1 watt.
Kilowatt (kW): One thousand watts.
Kilowatt-hour: One watt for 1000 hours; or
1000 watts for one hour; or 100 watts for 10 hours, etc. Unit
for recording electrical power use.
Energy: The ability to do work. Energy can
be neither created nor destroyed; it is a conserved quantity. It can, however,
be converted from one form to another.
Foot-pound: Unit for measuring work. It is
the energy required to move a weight of 1 pound through a distance of 1 foot.
Joule (J): The unit of work (W): force
acting through distance. One ampere X 1 volt X 1 second = 1
joule. One watt X 1 second = 1 joule. One coulomb X 1 volt = 1 joule.
Farad (F): The unit of capacitance (C). A
capacitor has a capacitance of 1 farad when one coulomb delivered to it will
raise its potential 1 volt. The farad is an impractically large quantity, so
you will hear more of microfarads, or
1/1,000,000 farad (10–6
farad).
Henry (H): The unit of electromagnetic
induction. A circuit possesses an inductance of 1 henry when a rate of current
variation of 1 ampere per second causes the generation therein of 1 volt.
Megawatt (MW): 1,000,000 watts; 106 watts.
Volt-amperes (VA): A term used to describe
alternating current; since we usually have opposition to the change of
direction of current in an alternating-current circuit, the volts and amperes
are very commonly out of phase. (This will be
explained
later.)
Kilovolt-amperes (kVA): One thousand
volt-amperes. Power Factor (PF): The phase displacement of volts and amperes in
an AC circuit due to capacitance and/or inductance. The cosine of the angle of
lag or lead between the alternating
current
and voltage waves. (This will be explained more fully later.)
Hertz (Hz): The new name for a cycle per
second. Alternation: One-half of a cycle. Frequency (of AC current): The number
of hertz completed.
Magnetic Units
The following definitions of magnetic
units are given mainly for later reference.
Gauss (G): Unit of magnetic flux density,
equal to one line of magnetic flux (maxwell) per square centimeter.
Maxwell (Mx): Unit of magnetic flux, one
magnetic line of flux.
Ampere-turn (At): The magnetomotive force
produced by a coil, derived by multiplying the number of turns of wire in the
coil by the current in amperes through it.
Oersted (Oe): Unit of magnetizing force
equal to 1000/4π ampere-turns per meter.
Permeability (µ): Expresses the ratio of
magnetic flux density produced in a magnetic substance to the magnetic field
intensity that occasions it.
Temperature Units
Celsius (°C): A temperature scale,
formerly termed centigrade and used extensively in electrical work and in the
metric system.
Fahrenheit (°F): A temperature scale
commonly used under our system of temperature recording. On the Celsius scale,
0°C is the temperature at which water freezes, and 100°C is the temperature at
which water boils. Both of these refer to sea level, or a barometric pressure
of approximately 14.7 pounds per square inch.
On the Fahrenheit scale, water freezes at
32°F and boils at 212°F. These, as with the Celsius temperature scale, are at
sea level. It is easy to convert from Celsius to Fahrenheit and from Fahrenheit
to Celsius.
For Example:
To convert 100°C to
Fahrenheit, take 9/5 of 100 and add 32; thus 9/5 of 100 = 180, and 180 + 32 =
212°F.
To convert 212°F to Celsius,
take 212 - 32 = 180, and take 5/9 of 180 = 100°C.
In electrical trade, much electrical equipment is rated in Celsius temperature
(°C), but in some cases the equipment may be rated in Fahrenheit (°F), or in a
combination of °C and °F.
Ohm’s Law and Power
There is another series of equations
related to Ohm’s law because of the fact that the power in watts in any
electrical circuit is equal to the current in amperes multiplied by the emf in
volts. Thus: where
P = power in watts
I = current in amperes
E = emf in volts
This formula may be transposed to find
either I or E. Thus:
I = P * E and E = P * I
So if P = 100 watts and I = 4 amperes, we
find E= P/I, or 100 W/4
A = 25 V. Since R = E/I and E = P/I, R = P/I^2, I^2 = P/R and I =
√P/R, and P = I^2R
Then, if P = 100 watts and R = 4 ohms,
then I^2 100 W/4 Ω = 25 A^2, and the square root of 25 is 5, so I=5
amperes. Further, since P=EI and I=E/R, we have:
E^2/R = P R = E^2 /P E^2 = RP and E = √RP
If R = 4 ohms and P = 100 watts, then
E2=PR = 100 W X 4Ω = 400 V2. The square root of 400 V^2 is 20 V. Thus,
E=20 volts.
Capacitance
The unit of capacitance is explained in
Chapter 2 and is designated by F. A capacitor thus has a capacitance of one
farad when one coulomb delivered to it will raise its potential one volt. The
farad is a very large unit of measurement, so we usually talk in terms of
microfarads (µF) or one one-millionth of a farad (10^-6 farad).
Let Q be the charge of a capacitor in
coulombs, E the applied potential difference in volts, and C the capacitance of
a capacitor in farads. Then
Capacitance = Charge / Potential Difference or C = Q/E
As previously stated, the capacitance of a
capacitor is affected by the material and dimensions of the dielectric. The
capacitance is directly proportional to the effective area of the dielectric
and inversely proportional to the thickness of the dielectric. Capacitance is
also proportional to the dielectric constant of the material between the
plates.
Let A be the total area of dielectric
between the plates, in square inches, s the thickness of dielectric in inches,
ĸ the dielectric
Capacitance = Charge /Potential Difference
or C = Q / E
Resistance
In the latter part of Chapter 1 a short
discussion on insulators and
conductors
was given. It was stated that there is no perfect insulator.
Also, a few metals in the order of their
conductivity appeared,
if
you wish to refer back to this part.
The word resistance comes from resist,
meaning to oppose. We may compare it to the friction of liquids flowing in
pipes. We have two water pipes, one 1⁄2 inch in diameter and one 1 inch
in diameter, both connected to the same source of water and both receiving the
same water pressure. The flow will be far less out of the 1⁄2-inch pipe
than out of the 1-inch pipe due to more friction (restriction) in the smaller
pipe. The basic principle is the
same
for conductors and resistance: Smaller conductors have more resistance and less
current-carrying capacity than larger conductors of the same material.
1. METRIC TERMS
a.
1,000,000,000 Billion – GIGA –G
b.
1,000,000 Million –
MEGA –M
c. 1,000 Thousand- Kilo –K
d. 1/1000 Thousandth – Milli –m
e. 1/1,000,000 Millionth - MICRO -µ
f. 1/1,000,000,000 Billionth - NANO – n
g. 1/1,000,000,000,000 Trillionth – PICO - p
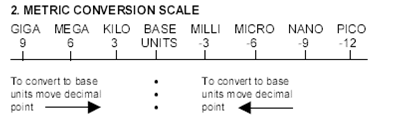
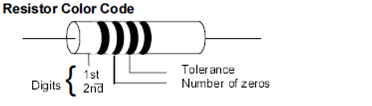
0 Black 4 Yellow 8 Grey
20% no color
1 Brown 5 Green 9 White
2 Red 6 Blue
5% Gold
3 Orange 7
Violet 10% Silver
Statement of
Ohm’s Law
The fundamental
statement of Ohm’s law is as follows:
The current in
amperes in any electrical circuit is numerically
equal to the electromotive force (emf
or voltage) in volts impressed
upon that circuit, divided by the
entire resistance of the circuit in
ohms. The equation may be expressed
where
I = intensity
of current in amperes
E = emf in
volts
R = resistance
in ohms
If any two
quantities of this equation are known, the third quantity
may be found by transposing, as
Analogy of Ohm’s Law Hydraulic analogies may be used to illustrate electrical
currents and the effect of friction (resistance).
We all know
from experience
E = I/R R =
E/I and I = E/R
4. DC Circuits
a. OHM’s law
E = IR
I = E/R
R = E/I
b. Resistors
in series
Rt = R1 + R2 + R3 + ….
It = I1 = I2 =
I3 = ….
Et = E1 + E2 + E3 + ….
c. Resistors
in parallel
Rt = R1 x R2 / R1 + R2
Rt = 1/ 1/R1 + 1/R2 + 1/R3 …
Different value resistors
R1 = R/N same
value resistors
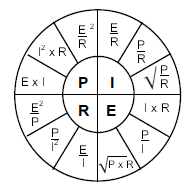
SYMBOLS
LETTER MEANING UNIT OF
SYMBOL MEASURE
E, V Voltage Volt
I Current Ampere
R Resistance Ohm
C Capacitor Farad
L Inductor Henry
X0 Capacitive Reactance Ohm
X1 Inductive Reactance Ohm
Z Impedance Ohm
Capacitor
a. Xc = 1/2πfC
b. Capacitors in a series add like resistors in parallel.
c. Capacitors in a parallel add like resistors in series.
Inductor
a. X = 2πfL
b. Inductors in a series add like resistors in parallel.
c. inductors in a parallel
add like resistors in series.
Time Constants
a. TC = RC Time it takes a capacitor to charge 63.2% of applied
voltage.
b. TC = L/R Time it takes an inductor to charge to 63.2% of available
current.
Where: T = Time constant in seconds
R = Resistance in ohms
C = Capacitance in farads
L = Inductance in henries
5T= Discharge or FULL charge
From Math * Logic Too Machine
All maths are composed of measure of
increase, and decrease the only changes are method, interpretation and symbol
designation. Integrating a solution would require the application of the rules
of integration and at the end would be addition and subtraction.
The computer by conducting Boolean algebraic
operations logic into their physical equivalents of electronic circuites
constructs and electrons flow control using various material properties.
Boolean algebra is a system of math which is capable of the 7 postulates of
math and solutions always only have two answers, yes or no. This solution set
is important because it turns out that minds perception of the world, as we
understand it has become increasingly binary. One or zero, yes and no or
discrete transition in energy levels as found in black body experimentations,
though not completely analogous statements, discrete states is the point here.
The Universe doesn't seem to be continuous or analogous at all but discrete. Or
at least we perceived it as such and there in lies our understanding of why the
mind works the way it does, mathematics and thus the way computers are
engineered to compute the way they do. Discretely,
sequentially and by iterative amounts or quantized.
The computer system operates at 2 discrete
levels to operate they are 0 and 1. This is called binary. The binary number
system combined with Boolean logic algebra is implemented with electronic
components to perform computer processing. Another numbering system is the
hexadecimal system.
Here is the binary system of counting:
Binary
0
• 1
•• 10
••• 11
•••• 100
••••• 101
•••••• 110
••••••• 111
•••••••• 1000
••••••••• 1001
This is the digits for the hexadecimal
numbering system is:

Hexadecimal numbers are less cumbersome to
deal with than binary numbers.
The binary counting system is capable of
all mathematical operations as a base 10 system but all operations result in
some series of zero or one. Here are some examples.
Rules of Binary Addition
* 0 + 0 = 0
* 0 + 1 = 1
* 1 + 0 = 1
* 1 + 1 = 0, and carry 1 to the next more
significant bit
For example,
00011010 + 00001100 = 00100110
Rules of Binary Subtraction
* 0 - 0 = 0
* 0 - 1 = 1, and borrow 1 from the next more
significant bit
* 1 - 0 = 1
* 1 - 1 = 0
Rules of Binary Multiplication
* 0 x 0 = 0
* 0 x 1 = 0
* 1 x 0 = 0
* 1 x 1 = 1, and no carry or borrow bits
Note:
The rules of binary multiplication are the same as the truths of the AND
gate.
Another Method: Binary multiplication is the same as repeated
binary addition; add the multicand to itself the multiplier number of times.
Binary Division
Binary division is the repeated process of
subtraction, just as in decimal division.
For example,
00101010 ÷ 00000110 = 00000111
Two Valued Boolean Algebra:
A two valued Boolean Algebra is defined on a set of two elements,
B = { 0, 1 }, with rules for the two binary operators +
and .
|
x |
y |
Xy |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
x |
y |
x+y |
|
|
0 |
0 |
0 |
|
|
0 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
1 |
1 |
1 |
|
|
x |
x' |
|
|
|
0 |
1 |
|
|
|
1 |
0 |
|
|
These rules are exactly the same as the AND, OR, & NOT operations,
respectively.
Now show that the Hunthington postulates
are valid for the set B = { 0, 1 } and the two binary
operators defined above.
1. Closure
The result of each operation is 1 or 0 and 1, 0 B.
2. From the table an identity element with respect to + is 0,
since 0 + 0 = 0
0 + 1 = 1 + 0 = 1
An identity element with respect to . is 1,
since 1.1
= 1
1.0 = 0.1 = 0
3. Commutative law
0 + 1 = 1 + 0 = 1 (
for + )
0
. 1 = 1
. 0 = 0 (
for . )
4. Distributive law
a. . is distributive
over + : x ( y + z ) = xy + xz
b. + is distributive over . :
x + ( y. z) = (x + y) . (x + z)
In summary, the binary number postulates are the following:
P1: X = 0 or X = 1
P2: 0 . 0 = 0
P3: 1 + 1 = 1
P4: 0 + 0 = 0
P5: 1 . 1 = 1
P6: 1 . 0 = 0 . 1 = 0
P7: 1 + 0 = 0 + 1 = 1
The table below outlines the system
|
x |
y |
Z |
y+z |
x.(y+z) |
x.y |
x.z |
xy + xz |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Once the binary arithmetic is understood
we can begin to use Boolean logic to manipulate this numbering system into
symbolic electric circuites, gates, adders and a myriad of other electronic
creations which permit computers to conduct its operations. But before we mathematically
build our computer, here are the rules.
Laws of Boolean Algebra
These are the basic
Boolean laws. Note that every law has two expressions, (a) and (b). This is
known as duality.
These are obtained by changing every AND(.) to OR(+),
every OR(+) to AND(.) and all 1's to 0's and vice-versa.
It has become conventional to drop the . (AND symbol) i.e. A.B is written as AB.
T1 : Commutative Law
(a) A + B = B + A
(b) A B = B A
T2 : Associate Law
(a) (A + B)
+ C = A + (B + C)
(b) (A B) C = A (B C)
T3 : Distributive Law
(a) A (B + C) = A B + A C
(b) A + (B C) = (A + B) (A +
C)
T4 : Identity Law
(a) A + A = A
(b) A A = A
T5 :
(a) ![]()
(b) ![]()
T6 : Redundance Law
(a) A + A B = A
(b) A (A + B) = A
T7 :
(a) 0 + A = A
(b) 0 A = 0
T8 :
(a) 1 + A = 1
(b) 1 A = A
T9 :
(a) ![]()
(b) ![]()
T10 :
(a) ![]()
(b) ![]()
T11 : De
Morgan's Theorem
(a) ![]()
(b) ![]()
Boolean functions are implemented by using electronic gates.
Mathematically they are stated as follows:
For 2 variables, n = 2, the number of possible BOOLEAN function is
16.
Truth tables
for the16 functions of two binary variables x& y.
|
x |
Y |
F0 |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
operator |
symbol |
|
. |
/ |
|
/ |
|
|
+ |
|
|
' |
|
' |
|
|
|
F1 represents the truth table for AND - the operator symbol is
.
F7 represents the truth table for OR - the operator symbol is +
Boolean expressions for the 16 function of two variables:
|
Boolean
function |
Operator
Symbol |
Name |
Comments |
|
F0 = 0 |
|
Null |
Binary
constant 0 |
|
F1 = xy |
x.y |
AND |
x
and y |
|
F2 = xy' |
x
/ y |
INHIBITION |
x
but not y |
|
F3 = x |
|
TRANSFER |
x |
|
F4 = x'y |
y
/ x |
INHIBITION |
y
but not x |
|
F5 = y |
|
TRANSFER |
y |
|
F6 = xy' + x'y |
x y |
EXCLUSIVE-OR |
x
or y but not both |
|
F7 = x + y |
x
+ y |
OR |
x
or y |
|
F8 = ( x + y )' |
x y |
NOR |
Not
- or |
|
F9 = xy + x'y' |
x y |
EQUIVALANCE |
x
equals y |
|
F10 = y' |
y' |
COMPLEMENT |
Not
y |
|
F11 = x + y' |
x y |
IMPLICATION |
If
y then x |
|
F12 = x' |
x' |
COMPLEMENT |
Not
x |
|
F13 = x' + y |
x y |
IMPLICATION |
If
x then y |
|
F14 = ( xy )' |
x y |
NAND |
Not
- And |
|
F15 = 1 |
|
IDENTITY |
Binary
constant 1 |
Electronic gates require a power supply. Gate INPUTS are driven by voltages having two
nominal values, 0V and 5V representing logic 0 and logic 1 respectively. The OUTPUT of a gate provides two nominal values
of voltage only, 0V and 5V representing logic 0 and logic 1 respectively. These
operations are tied to a timing circuit, the system clock.
The
gate components look like this:
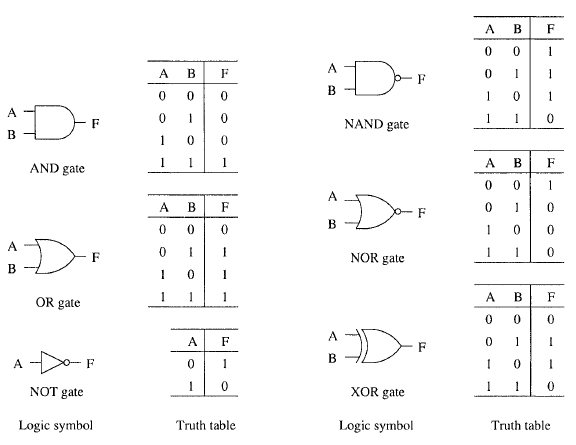
The table shows the implementation of
Boolean algebra using resistors and diodes.
These components are combined in packages
called chips. These chips look like this:
This is a single chip with imbedded components which form a circuit aka integrated circuit chips. These types of packages are calls specifically DIP (Dual Inline Package).
There are all kinds of circuits. They get very complicated and to date you can store millions of components on silicone wafers to form structure which look like cities on the head of a needle.
The MOS6502
In order to fully use a computer in a meaningful way you must know how it works. A detailed analysis of its design can be approached from top down, bottom up and inside out. A Top down view is concerned with how to use the computers resources, the programming model and interacting with it. A bottom up view is how the computer is designed in terms of its circuitry and components gates and an inside out view is concerned with how it works in terms of the interaction of the circuitry and its programing model.
The MOS6502 processor which as the heart of the Atari 2600, the Apple II and several Commodore PETS is very complex but pails in comparison to the complexity of modern day CPUs. It is an 8 bit architecture. Every memory access is a single cycle. The whole system is memory bound. Every assembly instruction has two cycles.
Here is some MOS6502 Code
Top Down
OP CMD
.,e000 85 56 STA $56 ;Store accumulator,regs A,X or Y
.,e002 20 0F BC JSR $BC0F ;Call instru, jump to sub routin
.,e005 A5 61 LDA $61 ;Load accumulator
.,e007 C9 88 CMP #$88 ;Comp A reg &
.,e009 90 03 BCC #E00E ;Branch if Carry clr
.,e00B 20 D4 BA JSR #BAD4 ;JUMP
.,e00E 20 CC BC JSR #BCCC ;JUMP
.,e011 A5 07 LDA $07 ;Load accumulator
.,e013 18 CLC ;Clear Carry Flag
.,e014 69 81 ADC #$81 ;Add,clear carry or it is added
.,e016 F0 F3 ADC #E00B ;Add
OP codes are 8 bits in size and is always 1 byte op code which encodes both the instruction and the addressing mode. The operand is always 0,1,2 bytes. CLC doesn’t have an operand so it’s a single byte and the jmp is a 3 byte instruction which references to a 16bit memory. Memory is 16 bits, 16 bits wide 16 bit address and there are three pages of memory. Some operations can only be accomplished in the first page.
The programming model includes the following




The first two pages of 256 bytes each goes to 0200FF addressable space. There are 64kb of addressable space. Stack is in the first page 01FF to 0100. The first page or zero page goes to 00FF it is meant for addressing modes if the address falls in this range then you have a special encoding.

64kb of addressable space. Stack is in the first page.

These are all the processor instructions that exist, here are a summary of their uses:
Load Instructions: LDA, LDX, LDY Load from memory into accumulator x, y, and a
Store : STA, STX, STY into memory
Transfer : TAX, TXA, TAY, TYA, TSX, TXS
Read Modify Write: ASL, LSR, ROL, ROR
Decrement, Increment: Decrement, Increment memory
Addition, Subtraction: ADC, SBC
Logic: AND, ORA, EOR
Compare: CMP, CPX, CPY subtraction that only stores bit
BIT: AND – stores flags and not result
Set Clear flags: CLV, SEC, CLC…
Branch: Branch depending on flags cleared, BMI, BPL, BVS, BVC…
Jump Unconditional: Jump subroutine, and interrupts JSR, BRK….
Stack: Only push the A register as well as the processor status register, PLA...
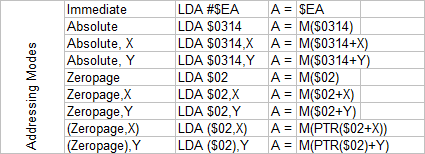

Immediate addressing has the hash sign. Load a constant in the accumulator LDA loads A. We have the constant of 17 in A.
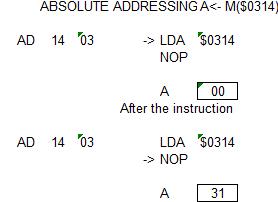
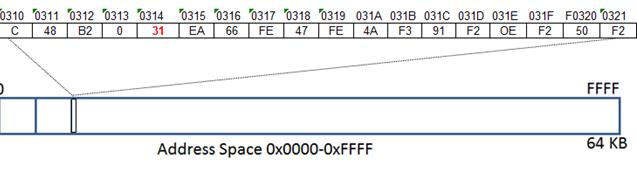
Absolute addressing uses a 16 bit operand($0314). You load from $0314 if you look in memory address at $0314 you have a constant of 31 and now a 31 in A.
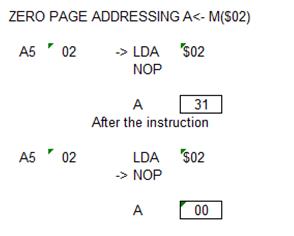
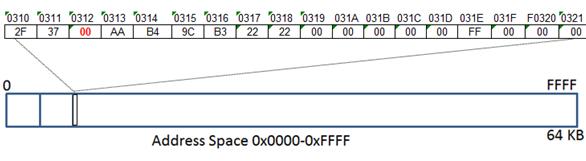
Zero page addressing takes a 8 bit operand. Load from address $02. Look it up in zero page, where we find 0. Therefore A = 0.

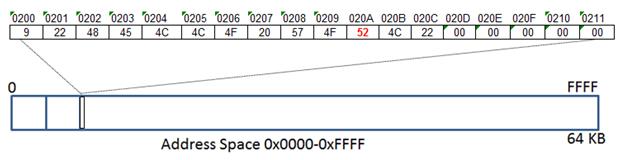
Absolute, X mean absolute plus X. So the X register gets added to the constant pointer that is encoded in the instruction stream. $0200,X if X = A in this example. Load from address 020A, which equals 52. At 0200 is an array of bytes and X is iterating over those.
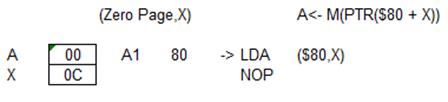
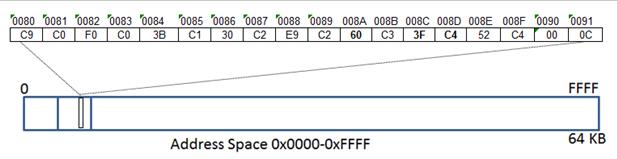
The indirection or pointer is accomplished without 16 bit registers. If you have a 16 bit pointer, you can’t hold it in a register. You must store the pointers in zero page. The way it is accomplished is the pointer is stored in zero page as a pointer. Addressing mode Zero Page, X(indirect) at $80 , in zero page, we index the array with X and then we load from of these pointers.

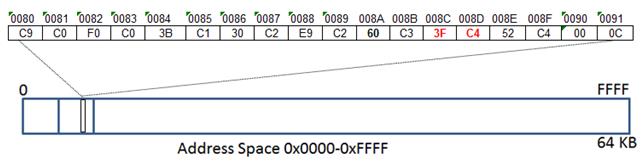
CPU looks at 0C index that address it gets the pointer it little indian. Its loaded from that address C43F does another look up and loads the 45 into A.
MOS6502 Stack
Stack is all implicit instructions. You initialize the stack to FF, or top of stack. If you push something on the stack it stores it first where the stack pointer points and then decrements the stack pointer.
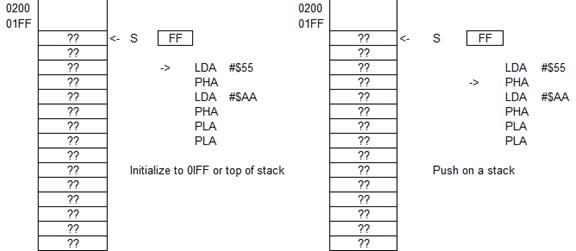
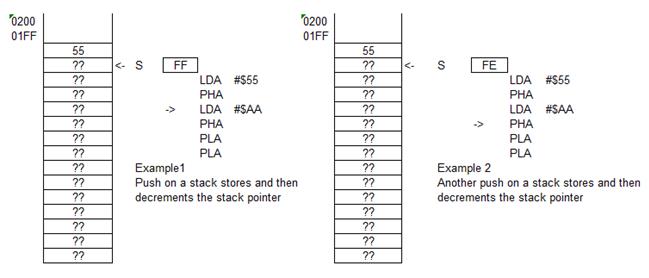
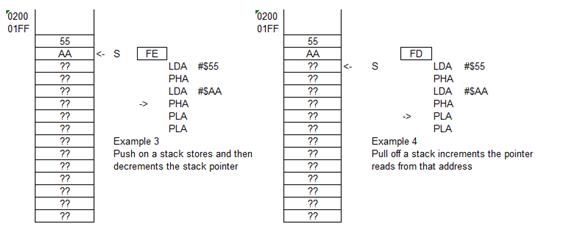
If you pull something off the stack it increments the stack pointer and then reads from that address.
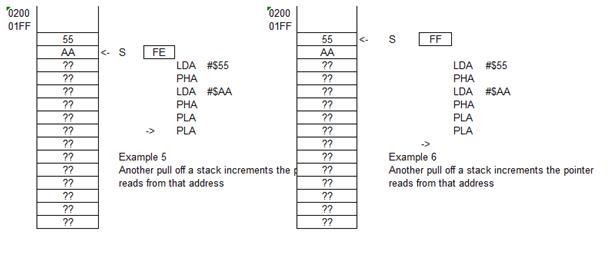
Again, pull something off the stack, it increments the stack pointer and then reads from that address.
There are oddities with the processor or quirks or even bugs. Incrementing in memory reads and then writes. But what it does is reads and then writes back the original value. Break instructions, used for debugging if preceded by an interrupt then the break is lost. The processes opcode array contains codes which are unknown or undefined which do everything from crash the computer to nothing at all.
Bottom Up
Datasheets of a process gives the processor timing schedules in term of it onboard components. They includes, netlists, schematic and timing diagrams.
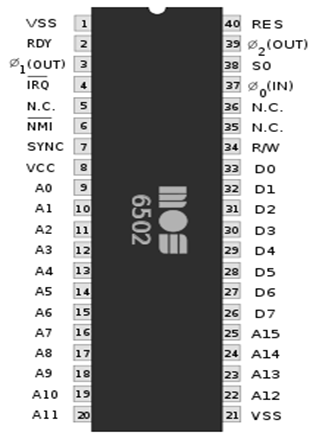
Pinout of the MOS6502
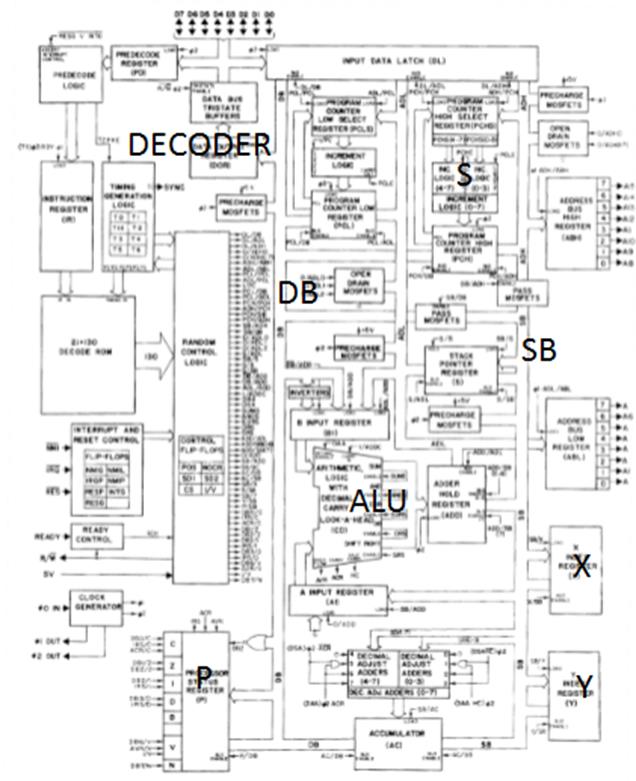
Schematic of the MOS6502
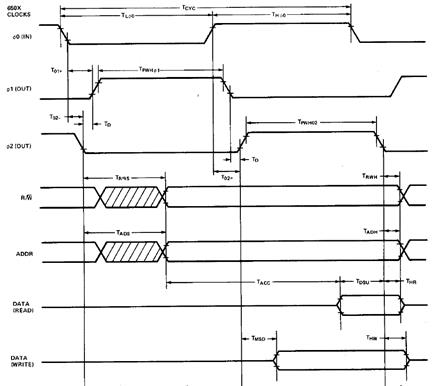
Timing Circuit
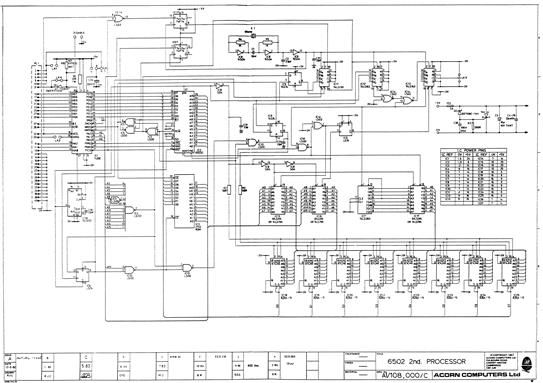
MOS6502 GATE LEVEL SCHEMATIC

Die shot of th MOS6502
From the Inside out
The MOS6502 is a very efficient processor. The simulating of the instruction cycles through the chip are beyond the scope of this text but is a fascinating look at the cycling of electronic flow through the circuitry due to clock cycle pulsed instructions fed to the chip.

Polygon representation of the MOS6502.
The 80x86 Microprocessor
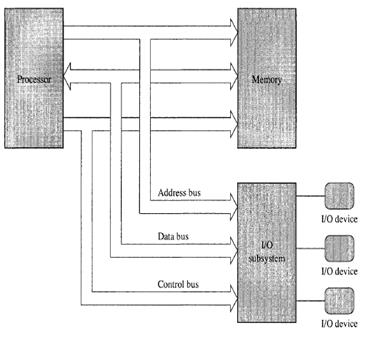
The 80x86 microprocessor uses the two's
complement notation. In the two's complement system, the H.O. bit of a number
is a sign bit. If the H.O. bit is zero, the number is positive; if the H.O. bit
is one, the number is negative.
The ASCII character set (excluding the
extended characters defined by IBM) is divided into four groups of 32
characters. The first 32 characters, ASCII codes 0 through 1Fh (31), form a
special set of non-printing characters called the control characters. We call
them control characters because they perform various printer/display control
operations rather than displaying symbols.
The computer processor’s functional design
looks like this:
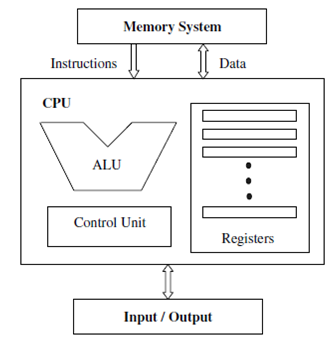
Notice how the processors functional
design is similar to the computer architectures overall design. This pattern of
design is the point here.
In the old days the way you programmed the
computer was to rewire the various functional circuits to conduct operations.
The wiring schemed looked like this.

CPU
Registers
CPU
registers are very special memory locations constructed from flip-flops.
They are not part of main memory; the CPU implements them on-chip. Various
members of the 80x86 family have different register
sizes. The 886, 8286, 8486, and 8686 (x86 from now on) CPUs have exactly four
registers, all 16 bits wide. All arithmetic and location operations occur in
the CPU registers.
Because
the x86 processor has so few registers, we’ll give
each register its own name and refer to it by that name rather than its
address. The names for the x86 registers are
AX
–The accumulator register
BX
–The base address register
CX
–The count register
DX
–The data register
Besides
the above registers, which are visible to the programmer, the x86 processors
also have an instruction pointer register which contains the address of
the next instruction to execute. There is also a flags register that
holds the result of a comparison. The flags register remembers if one value was
less than, equal to, or greater than another value. Because registers are
on-chip and handled specially by the CPU, they are much faster than memory.
Accessing a memory location requires one or more clock cycles. Accessing data in
a register usually takes zero clock cycles. Therefore, you should try to keep
variables
in the registers. Register sets are very small
and most registers have special purposes which limit their use as variables,
but they are still an excellent place to store temporary data. The patch panel
program wiring look like this.
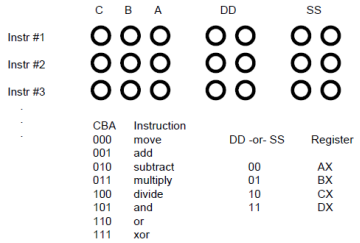
One
of the primary advances in computer design that the VNA(Von
Neumann architecture) is stored programming. One big problem with the patch
panel programming method is that the number of program steps (machine
instructions) is limited by the number of rows of sockets available on the
machine. John Von Neumann and others recognized a relationship between the
sockets on the patch panel and bits in memory; they figured they could store the
binary equivalents of a machine program in main memory and fetch each program
from memory, load it into a special decoding register that connected directly
to the instruction decoding circuitry of the CPU.
Logically
the modern computer registry circuitry is organized like this:
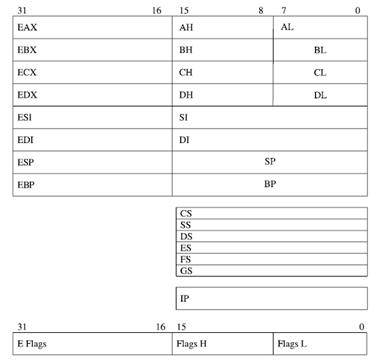
The
number of different opcodes varies widely from machine to machine. However,
the same general types of operations are found
on all machines. A useful and typical categorization is the following:
•
Data transfer
•
Arithmetic
• Logical
•
Conversion
•
I/O
•
System control
•
Transfer of control
Flag codes
The x86 CPUs do not complete execution of
an instruction in a single clock cycle. The CPU executes several steps for each
instruction. For example, the CU issues the following commands to execute the
mov reg, reg/memory/constant instruction:
Fetch the instruction byte from memory.
Update the ip register to point at the
next byte.
Decode the instruction to see what it
does.
If required, fetch a 16-bit instruction
operand from memory.
If required, update ip to point beyond the
operand.
Compute the address of the operand, if
required (i.e., bx+xxxx) .
Fetch the operand.
Store the fetched value into the
destination register
asm
file is the source code
lst
file is the list of opcodes
crt
file give the list of symbols and line numbers
op opcodes,
operands and
map
keeps tracks of segments
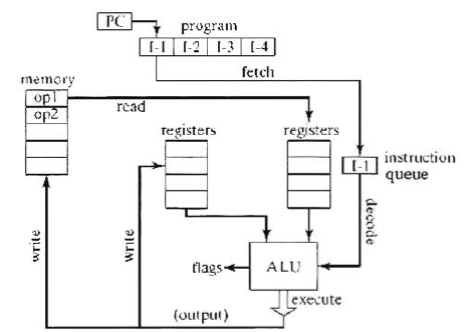
Finally, assembly programming on registry
operands looks like this. Note that mov is the same as copy.
mov ax, ax
mov ax, bx
mov ax, cx
mov ax, dx
In relation to the entire computer system
assembly language is next to machine level on the hierarchy of human to
computer interface.
Memmory location
(bytes) Binary Instruction Description
0000 0000 0000 0001 0000 0000 1100 Load the contents of location 12 in AC
0000 0000 0010 0011 0000 0000 0000 Move contents of AC to DR
0000 0000 0100 0001 0000 0000 1110 Load the contents of location 14 into
AC
0000 0000 0110 0101 0000 0000 0000 Add DR to AC
0000 0000 1000 0010 0000 0001 0000 Store contents of AC in location 16
0000 0000 1010 0000 0000 0000 0000 Stop
0000 0000 1100 0000 0001 0101 1110 Data value 350
0000 0000 1110 0000 0000 0110 0000 Data value 96
0000 0001 0000 0000 0000 0000 0000 Data value 0
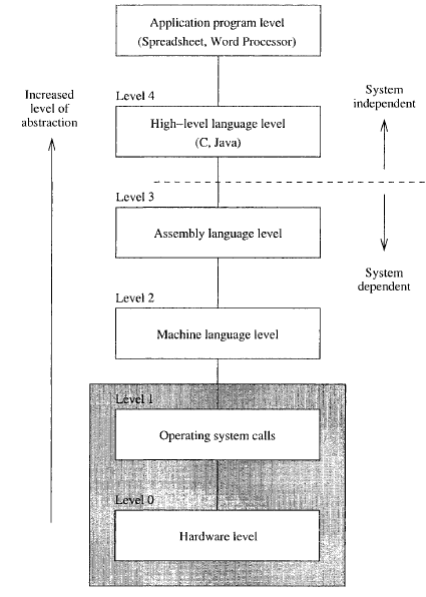
The C programming language is one level
upward and its statements are even more human readable. Here is an example:
#include <stdio.h>
int
main()
{
printf( "I am alive!
Beware.\n" );
getchar();
return 0;
}
It is important to remember that the
operating systems role is to control human to computer hardware interface.
Operating systems have been developed commercially. Commercial solutions are
proprietary, and internal details about design and implementation are not
publicly available. Though they are proprietary and interfaces to hardware may
be documented, the means by which the OS operates are often obscured and
hacking is required to fully understand how the proprietary OS really works.
Another important aspect of computer
architectures is how the processor interfaces with peripherals. Particularly the computer networking peripheral architecture.
Every peripheral device has a chip which has designated areas to be accessed by
the cpu. The devices makes requests to the cpu by processing known as interrupt calls. Network cards
are designed to generate signals that correspond to a system of OSI.
OSI Seven Layer Model
As shown, the OSI reference model is built,
bottom to top, in the following order: physical, data-link, network, transport,
session, presentation, and application. The physical layer is classified as
layer 1 and the top layer of the model, the application layer, as layer 7.

The OSI seven layer model.
Each layer of the OSI model has a specific
function. The following sections describe the function of each layer, starting
with the physical layer and working up the model.
Each protocol of the TCP/IP protocol suite
handles certain tasks within the TCP/IP protocol stack. Here is an overview of
the TCP/IP protocol stack and its protocols.
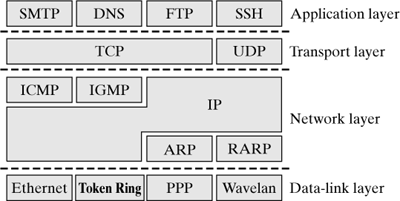
The protocols of the TCP/IP protocol
Standardized IP Packet Options
The IP packet options are appended to the
end of an IP header. The length of the Option field is variable, and the end of
a packet header has to be aligned to a 32-bit boundary, so an additional
padding field of the appropriate length is added (and set to 0 by default). In
this case, "variable" also means that the packet options can be left
out, if they are not required. The Option field can take one or several packet
options, where an option can be given in either of two formats:
One single byte describes only the option
type. The length of these options is always exactly one byte.
The first byte includes the option type,
and the second byte contains the length of this packet option. The following
bytes include the actual data of that option.
The IP packet header.
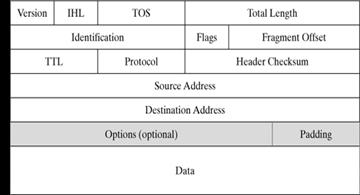
Data packets can contain tcp/ip protical coding for html.
The website request process.
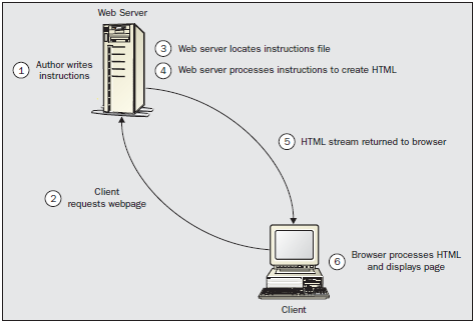
The HTTP Protocol
When a computer requests for a web page is
sent to the server, this request contains the desired URL information and three
other sections: the request/response line, the HTTP header, andthe HTTP body.
The content of these three sections is
dependent on whether the message is an HTTP request or HTTP response. Here is
the process:
HTML Example
<html>
<body>
<h1>My First Heading</h1>
<p>My first paragraph.</p>
</body>
</html>
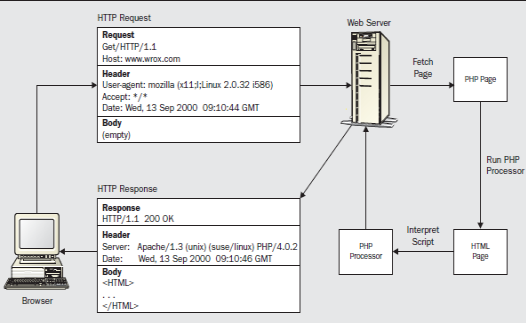
So, an example request line might look
like:
GET /testpage.htm HTTP/1.1 -
GET - This is a request for information
residing at a particular URL. The majority of HTTP requests made on the
Internet are GET requests. The information required by the request can be
anything from an HTML or PHP page, to the output of a JavaScript or Perl Script
program, or some other executable. You can send some limited data to the
browser, in the form of an extension to the URL.
HEAD - This is the same as the GET method,
except that it indicates a request for the HTTP header only and no data.
POST - This request indicates that data
will be sent to the server as part of the HTTP body. This data is then transferred
to a data-handling program on the web server.
There are a number of other methods
supported by HTTP – including PUT, DELETE, TRACE, CONNECT, and OPTIONS. The RFC 2068 at http://www.rfc.net
containes a complete list of specifications.
The HTTP Header The
next bit of information sent is the HTTP header. This contains details of what
document types the client will accept back from the server, like the type of
browser that has requested the page, the date, and general configuration
information. The HTTP request's header contains information that falls into
three different categories:
General: contains information about either
the client or server, but not specific to one or the other.
Entity: contains information about the
data being sent between the client and server Request: contains information
about the client configuration and different types of acceptable documents.
An example HTTP header might look like
this:
Accept: */*
Accept-Language: en-us
Connection: Keep-Alive
Host: www.wrox.com
Referer: http://webdev.wrox.co.uk/books/SampleList.php?bookcode=3730
User-Agent: Mozilla (X11; I; Linux 2.0.32
i586)
The HTTP header is composed of a number of
lines; each line contains the description of a piece of HTTP header
information, and its value. There are many different lines that can comprise a
HTTP header, and most of them are optional, so HTTP has to indicate when it has
finished transmitting the header information. To do this, a blank line is used.
In HTTP 1.1, a request must comprise of at least a request line and a HOST
header.
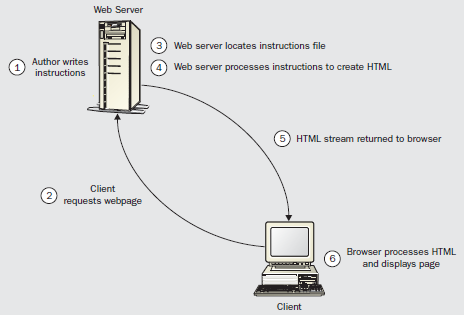
The only difference comes when, in the act
of preparing a page to be sent to the browser, the server comes across a
script. The first thing the server must do is identify the machine responsible
for processing the script. This is an important point because, when we write a
script, we can choose whether it is to be processed by the server or by the
browser. A script that is interpreted by the web server is called a server-side
script. A server-side script is an instruction set that is processed by the
server, and generates HTML. The resulting HTML is sent as part of the HTTP
response to the browser. The browser lays out the HTML page via HTML, PHP,
Javascript and/or other script based on the browser internal API Interface or
Document Object Model(DOM) and displays it
accordingly.
What is the DOM?
The Document Object Model (DOM) is a
programming interface for HTML and XML documents. It provides a structured
representation of the document and it defines a way that the structure can be
accessed from programs so that they can change the document structure, style
and content. The DOM provides a representation of the document as a structured
group of nodes and objects that have properties and methods. Essentially, it
connects web pages to scripts or programming languages. A pure HTML page is
interpreted by the browser. HTML is not processed by the web server. Instead,
it is sent to the browser (as part of the HTTP response) and is processed by
the browser; the result is then displayed by the browser.
A Web page is a document. This document
can be either displayed in the browser window, or as the HTML source. But it is
the same document in both cases. The Document Object Model (DOM) provides
another way to represent, store and manipulate that same document. The DOM is a
fully object-oriented representation of the web page, and it can be modified
with a scripting language such as JavaScript, PHP, and Java Sever Pages(JSP), the only diference is where this takes place.
Some languages, like javascript, work at the user application level like a web
browser. Others like JSP and PHP accesses the user DOM at the server level.
The W3C DOM standard forms the basis of
the DOM implemented in most modern browsers. Many browsers offer extensions
beyond the W3C standard, so care must be exercised when using them on the web
where documents may be accessed by various browsers with different DOMs.
All of the properties, methods, and events
available for manipulating and creating web pages are organized into objects
(e.g., the document object that represents the document itself, the table
object that implements the special HTMLTableElement DOM interface for accessing
HTML tables, and so forth). This documentation provides an object-by-object
reference to the DOM implemented in Gecko-based browsers.
API (web or XML page) = DOM + JS
(scripting language)
The DOM was designed to be independent of
any particular programming language, making the structural representation of
the document available from a single, consistent API. Though we focus
exclusively on JavaScript in this reference documentation, implementations of
the DOM can be built for any language, as this Python example demonstrates:
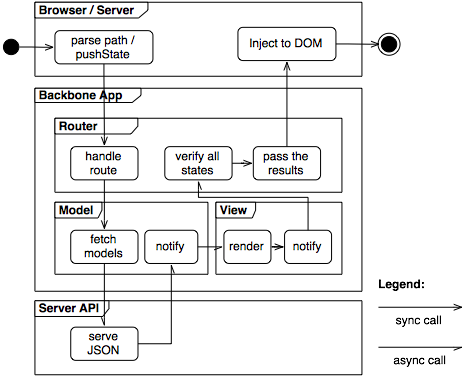
In PHP the server passes the result to the
result back to the DOM in the requesting browser which redenders the page.
Here, everything contained within the <?php and the ?> is assumed to be PHP, and is sent to the
PHP script engine for processing. So, in our example, once the PHP is processed
it is returned to the browser as HTML, and indeed if
you
look on the browser's View Source option you should see that the program has
been returned to you in pure HTML.
Learning is the process of changing mental
landscapes. Here how it works. Imagine that the peripheral vision was obscured
and a wall ten feet high, and thirty feet wide with measurement markers was
placed on the ground in front of you. If you were asked to measure the wall you
would find it difficult. If you were raised 60 feet in the air you would have a
perspective that gave you the breadth width and scope of the wall and would
also allow you to see the markers in context. You wouldn’t even need the view
if you understood the context of and nature of the wall by understanding the
law of walls. The law of walls may be understood without formal learning by observation
and understanding of apparently unrelated observations of similarly colored,
tactile, and composition of the materials of the wall. Politics would bring
about an approved system of description or delusion and communicated to others
about the nature of walls and so forth and thus learning and inference on the
nature of things and that of wall is performed.
This process of changing ones minds
landscape leads to broader understand and ignorance than rote learning is
capable of achieving. What is the purpose of a thing? What is its nature? This
change of understanding patterns or landscape shifting of the minds conception,
not the agitation of perception and consumption of information for informations
sake is the most effective prediction enabling and ground breaking paradigm
forming imputus of learning.
It’s how one can infer existence without
direct experimental evidence. This is important because some things are
theoretically impossible to see directly but must be conceived to be perceived.
Patterns of and Cues of the Conceived Eye
You are alive and the cues are everywhere.
What are the dimensions of the space? What are the spaces of the inhabitants?
Inherent cues arise from the direct cues. They are temporal (past, present
future), in respect to the supporting structures which are material (human,
inert, conceiving), contextual (ambient ripples). What are the supporting
materials, subliminal and social context which bind the space? What are the
cues of ones role in the space and the response to change of your internal
space and the landscape rippling response to the change? Trace the wiring in
the ceiling grid and rediscover the effort and achievement and the signatures
of the overt effort of the controlled orchestration of cues to impose upon the conceived
mind. All orchestrated patterns of repetition and coding designed to prepare
the conceiving mind to assume a state conducive of the perpetuation of mind.
Learning causes changes potential for
behavior. Learning comes in two flavors, latent and actual and is the result of
perception.
Illegal op codes
Some programming consists of illegal
codes. These shortcuts can be used. Life is the same way. Not in terms of doing
illegal things in terms of the law but using the whole landscape and taking
advantage of shortcuts.
Programming in C++
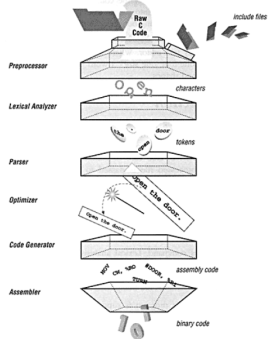
C plus is a mid level language which is
used to pass instruction to a computer by a process called programming. A set
of commands are written or its equivalent designed into a chip and the computer
runs the program. Running of a program is initiated by loading the contents of
an executable code file into memory, using a loader. The loader is usually an
integrated part of the operating system. These programs are translated into
machine language through a varying number steps by compiling. Here are some of
the steps:
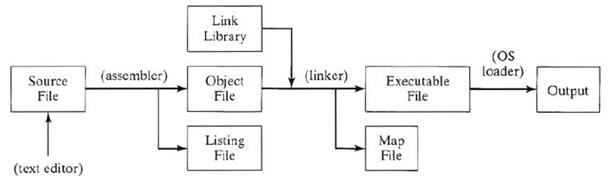
Compiling C
• Source program processing starts by
reading the entire program into a character buffer. This simplifies memory
management, token isolation, file position tracking, and error reporting.
• Lexical analysis turns a stream of
characters into a stream of tokens;
Syntax analysis turns a stream of tokens
into a parse tree, or, more probably, an abstract syntax tree. Together they
undo the linearization the program suffered in being written out sequentially.
• Often, identifiers recognized by the
lexical analysis have to be identified further before being passed to the
syntax analyzer. They are looked up in the symbol table. This identification
can serve type identifier identification, keyword identification, macro
processing, conditional compilation, and file inclusion.
• Macro substitution, macro parameter
expansion, conditional compilation, and
file
inclusion can be implemented simultaneously using a single stack of input
buffers.
• Code generation converts the
intermediate code into symbolic machine instructions in a paradigm-independent,
language-independent, and largely machine independent process. The symbolic
machine instructions are then converted to some suitable low-level code: C code,
assembly code, machine code.
Code generation yields a list of symbolic
machine instructions steps away from an executable binary program. In most
compilers, these steps are delegated to the local assembler
• An assembler converts from symbolic
machine code to binary machine code, and
from
symbolic data to binary data. In principle the conversion is one to one; The assembler then produces a binary version of it and
places it in the proper position in the object file, together with the code and
data segments, the relocation bit maps, and possibly further header and trailer
material.
• The linker reads each object file. This
yields one code segment, one data segment, one relocation bit map, and one
external symbol table, each consisting of the concatenation of the
corresponding components of the object files. In addition the linker retains
information about the lengths and positions of the various components. It is
now straightforward to do the relocation of the internal addresses and the
linking of the external addresses; this resolves all addresses. The linker then
writes the code and data segments to a file, the executable code file;
optionally it can append the external symbol table and debugging information.
Programing in C\C++ vs Assembly Language
Learning what computer programming is can
be quit a challenge. Here is the dilemma that every beginner programmer will
face. How you look at a written computer program for the first time can cost
you years of brain damage. So here is what a computer program is not.
There is no logic here. Looking at the
syntax and grammar of a program will trick you into thinking there is a flow or
pattern that makes the computer behave. No, don’t look at it that way. The
reason this approach is fraught with pitfalls is because programming allows for
many writing styles. There are contests for writing horrible looking unreadable
code that can be compiled into meaningful programs. The key is that you are
entering a succession of strings like a writing to a dos prompt that will be
read by a lexar of a compiler. A linker will then create an executive file for
a targeted os. The c compiler and the target os rules and you will have to
create code that compiles successful and does something meaningful.
The software you write is more than the sum of its parts. If you
have ever played Snake and then looked at its source code you can appreciate
that the simple game is fun as hell and the simple game is complicated as hell
to implement. It is the soul of the effort. The code when completed will create
something very enjoyable if it is meaningful and if you are good the code will
appear deceptively simple and even elegant. Don’t bother learning every c
function or windows api or linux whatever, there are
too many. Learning every math formula didn’t get Einstein to Relativity. He had
a vision and used and learned new math to implement an elegant and invaluable
theory that was good then and now.
You will not code any major software
project alone. There are armies of programmers in trenches working hard as hell
to produce many of the products that have inspired you, instead, look at the
software endeavor as a great little puppy. Feed it, protect it and grow it and
if you can afford a trainer, a groomer and some other help give the puppy (your
software) the best life it can have.
Let’s look at c programming from the top
down, bottom up and inside out. The circuitry of the computer employs various
types of circuits to compute. Adders, Latches and combination
circuits, etc. These circuits by attributes of the circuitry design
create register memory, stack memory, alu operations, flags, execution, clocks,
etc. These operations are binary, and hexadecimal and can encoded by a one to
one human readable mnemonic system like assembly language and CPU op codes. The
mnemonics organize the computer resources by there functions. The primary
functions are movs(copy), push(save a value on memory type stack), pops(read a
value off stack), labels, db(data), tests, calls, jumps, shifts, logic,
arithmetic, calls, returns, special os and bios system codes and a few hundred
more operations. This is the domain in which all higher level language
convention exists.
Intel x86 Assembly Language Keywords
add and call cld cli cmp cmpb db
dd dec decb dw equ global in inb
inc incb ins int iret ja jae jb
jbe jg jge jl jle jmp jnz jz
lea lgdt lidt lldt loop ltr mov movs
movsb movzx neg nop o16 or out outb
outs pop popad popf push pushad pushf rep
ret rol ror section sgdt shl shr std
sti stos sub test times xchg xor
To code in assembly code, you must,
shift(add,divide, etc), mov(copy) operands into memory locations, test the
results with flags, call hard wired functions, lable operations, ret(return)
and exit the program.
C operators
The standard C language provides the
following operators and punctuators:
{ } [ ] ( ) (type) .
-> ++ -- & * + - ~
! sizeof / % << >> < > <= >= == !=
^ &&
|| ? : = *= / = %= += -= <<=
>>= &= ^= |=
, # ## ; : " "
ANSI
C (C89)/ISO C (C90) keywords:
auto
double int struct
break else
long switch
case enum register
typedef
char
extern return union
const
float short unsigned
continue for signed void
default
goto sizeof volatile
do if
static while
The standard header files
that comes with c are.
SO/IEC 9899:1990 (C89, C90) - ISO/IEC
9899:2011
<assert.h> <limits.h> <signal.h> <stdlib.h>
<ctype.h> <locale.h> <stdarg.h> <string.h>
<errno.h> <math.h> <stddef.h> <time.h>
<float.h> <setjmp.h> <stdio.h> <tgmath.h>
<iso646.h> <wchar.h> <wctype.h> <uchar.h>
<complex.h> <inttypes.h> <stdint.h> <threads.h>
<fenv.h> <stdbool.h> <stdnoreturn.h> <stdatomic.h>
<stdalign.h>
The c programming language is an attempt
at hardware independence as assembly language is hardware dependent and must be
written to a specific hardware and os. Some books say that the language is more
readable and this is true. The problem is that readability gives the user the
illusion of literality. The coding is still based on the machines one to one
architecture and the compiler interprets your programs into machine code which
is hard for humans to manipulate. This is important to understand because
debugging sometimes arises from the compiler misinterpreting your program
procedures.
In c you code in statement format. The
accounting for memory and testing is hidden behind math symbols and c grammar.
Its still there it’s just translated by the compiler. If you look at c code you
can see assembly language operations peaking under the surface with a little
imagination.
C Plus is a different language. It is
written in sentence format just like c but the grammar is a bit different and
some enhancements to code management have been added. These “enhancements” are
referred to as object orientated programming.
C++ Keywords
Asm auto bool break case
catch
char class const_cast continue
default delete
do
double else
enum dynamic_cast
extern false float
for
union unsigned using
friend
goto if
inline int
long
mutable virtual
namespace new operator
private protected
public register void
reinterpret_cast
return short signed sizeof
static static_cast volatile struct switch
template this throw true
try
typedef typeid
unsigned wchar_t while
ISO/IEC 14882:2011 (C++2011)
The 52 C++ headers are:
<algorithm> <fstream> <list> <regex> <typeindex>
<array> <functional> <locale> <set> <typeinfo>
<atomic> <future> <map> <sstream> <type_traits>
<bitset> <initializer_list> <memory> <stack> <unordered_map>
<chrono> <iomanip> <mutex> <stdexcept> <unordered_set>
<codecvt> <ios> <new> <streambuf> <utility>
<complex> <iosfwd> <numeric> <string> <valarray>
<condition_variable> <iostream> <ostream> <strstream> <vector>
<deque> <istream> <queue> <system_error>
<exception> <iterator> <random> <thread>
<forward_list> <limits> <ratio> <tuple>
The 26 headers related to C (C2011) are:
<cassert> <cinttypes> <csignal> <cstdio> <cwchar>
<ccomplex> <ciso646> <cstdalign> <cstdlib> <cwctype>
<cctype> <climits> <cstdarg> <cstring>
<cerrno> <clocale> <cstdbool> <ctgmath>
<cfenv> <cmath> <cstddef> <ctime>
<cfloat> <csetjmp> <cstdint> <cuchar>
C++ OPERATORS
Level Precedence
group Operator Description Grouping
1 Scope :: scope qualifier Left-to-right
2 Postfix
(unary) ++ -- postfix increment / decrement Left-to-right
() functional forms
[] Subscript
. -> member access
3
Prefix (unary) ++ -- prefix increment / decrement Right-to-left
~ ! bitwise NOT /
logical NOT
+ - unary prefix
& * reference / dereference
new
delete allocation / deallocation
sizeof parameter pack
(type) C-style type-casting
4 Pointer-to-member . * ->* access
pointer Left-to-right
5 Arithmetic:
scaling * / % multiply, divide, modulo Left-to-right
6 Arithmetic:
addition+ - addition, subtraction Left-to-right
7 Bitwise
shift
<< >> shift left,
shift right Left-to-right
8 Relational
< > <= >= comparison
operators Left-to-right
9 Equality
== != equality
/ inequality Left-to-right
10 And
& bitwise AND Left-to-right
11 Exclusive
or ^ bitwise
XOR Left-to-right
12 Inclusive
or | bitwise
OR Left-to-right
13 Conjunction
&& logical AND Left-to-right
14 Disjunction || logical OR Left-to-right
15 Assignment-level
expressions = *= /= %= += -=
>>= <<= &= ^= |= assignment
/ compound assignment Right-to-left
?: conditional operator
16 Sequencing , comma separator Left-to-right
The c language has a grammar right? So how
do you read it.
Coding in c has rules that the compiler
enforces. Rules can be manipulated when they are understood.
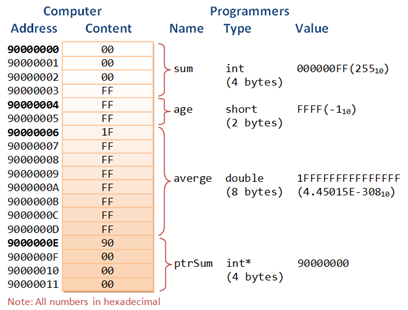
Pointers and referrrences are aggravating as shit.
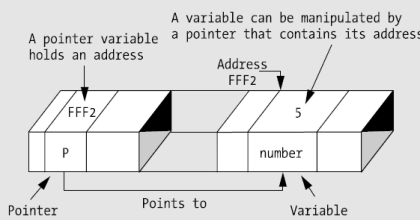
int number = 88; // An int variable with a value
int * pNumber; // Declare a pointer variable called
pNumber pointing to an int (or int pointer)
pNumber =
&number; // Assign the address of
the variable number to pointer pNumber
int * pAnother = &number; // Declare another int pointer and init to address of the variable number
A reference works as a pointer. A reference is declared as an alias of a variable. It stores the address of the variable, as illustrated:
Here is another illustration of a
reference variable.
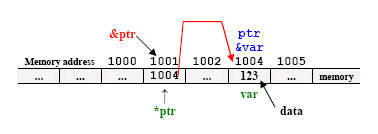
Here
is some C code.
int number = 88;
int * pNumber =
&number; // Declare and assign the
address of variable number to pointer pNumber (0x22ccec)
cout <<
pNumber<< endl; // Print the
content of the pointer variable, which contain an address (0x22ccec)
cout << *pNumber
<< endl; // Print the value "pointed to" by the pointer, which
is an int (88)
*pNumber = 99; // Assign a value to where the
pointer is pointed to, NOT to the pointer variable
cout << *pNumber
<< endl; // Print the new value "pointed to" by the pointer
(99)
cout << number
<< endl; // The value of variable
number changes as well (99)
*ptr
- a pointer variable
var -
a normal variable
// declare a pointer variable ptr of type
int
int
*ptr;
// declare and initialize normal variable
var of type int
int
var = 123;
// assign the address of normal variable
var to pointer ptr.
ptr
= &var;
*
- is a pointer to
[ ] - is an array of
( ) - is a function returning
&
- is an address of
int *x
x is a pointer to int data type.
int *x[10]
x is an array[10] of pointer to int data type.
int *(x[10])
x is an array[10] of pointer to int data type.
int **x
x is a pointer to a pointer to an int data type – double pointers.
int (*x)[10]
x is a pointer to an array[10] of int data type.
int *funct()
funct is a function returning an integer pointer.
int (*funct)() funct is a pointer to a function
returning int data type – ………………………………………..quite
familiar constructs.
int (*(*funct())[10])() funct is a function
returning pointer to an array[10] ………………………………………..of pointers to functions returning
int.
int (*(*x[4])())[5] x is an array[4] of pointers to functions
returning pointers to array[5] of int.
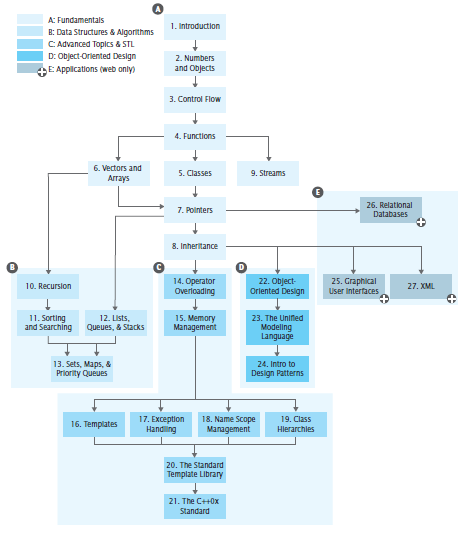
Programming with a flow chart like truth
table or circuitry diagram is helpful when programming software.
The soul of the program –
what is the psychology effect to convey. Putting the atoms together to make meaning. Math required to convey human experience meaningful experience. Here are
the steps to programming.
- Start with the idea.
- I want to print a message.
- Research the built in function that achieve this and if not
build your own. In C print() function is used to
display messages. In order to use the built in function you have to
include it. #include <stdio.h>.
Here is the skeleton C
#include <stdio.h>
int
main()
{
}
Here is how you use the included C print
function.
#include <stdio.h> // include statement imports makes these
pre packaged ……………………………………………………………………..functions
available. Otherwise you would have to ……………………………………………………………………..write
your own c/assembler function to handle ……………………………………………………………………..console
output. NO!
int
main() //Every program has
main.
{ //braces are for C grammar, compiler doesn’t need
printf("This is output from my first program!\n");
// print, YES!! Use it
return 0;
//Every C program returns control to OS.
} //..but
humans need and compiler will error if not here
Idea 2
Lets
add two integers. I want to print two added integers. Research the built in
function that achieve this and if not build your own. In C print()
function is used to display messages. Strategy is to store values into memory
variable and instruct and add of those variables and then print the result.
Prototype:
#include <stdio.h>
int
main()
{
int
x;
int
y;
int
z;
z = x + y;
printf("%d\n", z);
return 0;
}
Answer was a memory address but it worked!
Why?
Ok prototype compiled, lets
add some values or initialize the variables.
#include <stdio.h>
int
main()
{
int
x = 1;
int
y = 2;
int
z;
z = x + y;
printf("%d\n", z);
return 0;
}
Ok answer was 3. It worked!
Lets
permit the program to prompt for a value. Scanf()
function will works.
#include <stdio.h>
int
main()
{
int
x = 1;
int
y = 2;
int
z;
int
t;
scanf("%d",
&t); // Here is the function
z = x + y + t;
printf("%d\n", z);
return 0;
}
Entered a 3 got a 9.
Ok lets test a
value. Lets use the while(){};.
#include <stdio.h>
int
main()
{
int
x = 1;
int
y = 2;
int
z;
int
t;
scanf("%d",
&t);
if(t
!= -1){
z = x + y + t;
printf("%d\n",
z);
};
return
0;
}
If you don’t enter –1 the program will
execute. It works. Now let’s add a function to call to add for us.
#include <stdio.h>
int
addnum(int, int, int);
int
main()
{
int
x = 1;
int
y = 2;
int
z;
int
t;
scanf("%d",
&t);
if(t
!= -1){
z = addnum(x , y
, t);
printf("%d\n",
z);
};
return
0;
}
int
addnum(int e, int f, int g) {
return
e + f + g;
}
Ok it worked. Lets
store the values in an array.
#include <stdio.h>
int
addnum(int w[], int arrayreferences);
int
main()
{
int
x = 1;
int
y = 2;
int
z;
int
t;
int
a[2] = {x, y, t};
scanf("%d",
&t);
if(t
!= -1){
z = addnum(a, 2);
printf("%d\n",
z);
};
return
0;
}
int
addnum(int v[], int arrayreferences) {
int
i, sum=0;
for
(i=0; i<arrayreferences; i++){
sum = sum + v[i];
}
return(sum);
}
Ok lets use a
pointer to a memory location that stores a value.
#include <stdio.h>
int
addnum(int w[], int arrayreferences);
int
main()
{
int
x = 1;
int
y = 2;
int
z;
int
t;
int
a[2] = {x, y, t};
scanf("%d",
&t);
if(t
!= -1){
z = addnum(a, 2);
int
*zPtr;
zPtr
= &z;
printf("%d\n",
*zPtr);
};
return
0;
}
int
addnum(int v[], int arrayreferences) {
int
i, sum=0;
for
(i=0; i<arrayreferences; i++){
sum = sum + v[i];
}
return(sum);
}
It worked. Lets
return pointers from a function
#include <stdio.h>
int
addnum(int *w[], int arrayreferences);
int
main()
{
int
x = 3;
int
y = 2;
int
z;
int
t;
int
a[2] = {x, y, t};
scanf("%d",
&t);
if(t
!= -1){
z = addnum(a, 2);
int
*zPtr;
zPtr
= &z;
printf("%d\n",
*zPtr);
};
return
0;
}
int
addnum(int *v[], int arrayreferences) {
int
i, sum=0;
for
(i=0; i<arrayreferences; i++){
sum = sum + v[i];
int *sumPtr;
sumPtr = ∑
}
return(sum);
}
Ok we returned a pointer to the final
value from the function. Lets work with chars.
#include <stdio.h>
#include <stdlib.h>
main(){
int i;
char *cp;
cp = "a string";
while(*cp != 0){
putchar(*cp);
cp++;
}
putchar('\n');
for(i = 0; i < 8; i++)
putchar("a
string"[i]);
putchar('\n');
return(0);
}
Ok it worked. Lets
do this with a struct.
#include <stdio.h>
struct
teststruct {
char *cp;
};
main(){
struct teststruct a;
struct teststruct *aPtr;
a.cp = "a string";
aPtr = &a;
while(*a.cp != 0){
putchar(*a.cp);
*a.cp++;
}
putchar('\n');
return(0);
}
Computers only 0’s and 1’s.
Storage of memory variables are temporary if stored in
ram. In ordinary to retrieve it for later use it must be stored on a secondary
disk. Data items are hierarchy. Lets make a file.
#include <stdio.h>
int
main() {
int account;
char name[30];
double balance;
FILE *cfPtr;
if (( cfPtr = fopen("client.dat", "w"))
== NULL)
printf("file could not be opened");
else {
printf("Enter the account, name, and
balance.\n");
printf("Enter EOF to end input\n");
printf("? ");
scanf("%d%s%lf", &account, name,
&balance);
while(!feof(stdin)){
fprintf(cfPtr, "%d %s %.2f\n",
account, name, &balance );
printf("? ");
scanf("%d%s%lf", &account, name,
&balance);
}
fclose(cfPtr);
}
return 0;
}
Data structure
#include <stdio.h>
#include <stdlib.h>
struct
listNode {
char
data;
struct
listNode *nextPtr;
};
typedef
struct listNode ListNode;
typedef
ListNode *ListNodePtr;
void
insert(ListNodePtr *, char);
char
delete(ListNode *, char);
int
isEmpty(ListNodePtr);
void
printList(ListNodePtr);
void
instruction(void);
main()
{
ListNodePtr startPtr = NULL;
int
choice;
char
item;
instrucions();
printf("?
");
scanf("%d",
&choice);
while
(choice !=3 ) {
switch(choice != 3){
case
1 :
printf("Enter a character: ");
scanf("\n%c", &item);
insert(&startPtr);
break;
case
2:
if (!isEmpty(startPtr)) {
printf("Enter character to be deleted:
");
scanf("\n%c", &item);
if (delete(&startPtr, item)) {
printf("%c delete.\n", item);
printList(startPtr);
}
else
printf("%c not found.\n\n", item);
}
else
printf("List is empty.\n\n");
break;
default:
printf("Invalid choice.\n\n");
instructions();
break;
}
printf("? ");
scanf("%d", &choice);
}
printf("Enter
of run.\n");
return
0;
}
void
instructions(void) {
printf("Enter
your choice:\n"
" 1 to insert an
element into the list.\n "
" 2 to delete an
element from the list.\n"
" 3 to
end.\n");
}
void
insert(ListNodePtr *sPtr, char value) {
ListNodePtr newPtr, previousPtr,
currentPtr;
newPtr
= malloc(sizeof(ListNode));
if
(newPtr != NULL) {
newPtr->data = value;
newPtr->nextPtr = NULL;
previousPtr = NULL;
currentPtr = *sPtr;
while (currentPtr != NULL && value >
currentPtr->data){
previousPtr = currentPtr;
currentPtr = currentPtr->nextPtr;
}
if (previousPtr == NULL){
newPtr->nextPtr = *sPtr;
*sPtr = newPtr;
}
else {
previousPtr->nextPtr = newPtr;
newPtr->nextPtr = currentPtr;
}
}
else
printf("%c not inserted. No memory
available.\n", value);
}
char
delete(ListNodePtr *sPtr, char value){
ListNodePtr previousPtr, currentPtr,
tempPtr;
if(value
== (*sPtr)->data){
tempPtr
= *sPtr;
*sPtr = (*sPtr)->
nextPtr;
free(tempPtr);
return
value;
}
else
{
previousPtr = *sPtr
}
}
}
}
};
Comments are talking to the human. Print
statements are giving cues to the human for human interaction. The game or
program is cuing the human for interaction. Just keep witting. Name the values
in an illustrative way to speak to your audience. Talk to those following
audience and connect. Talk don’t fight. You are
swimming in a digital ocean, give your self beacons to get back and know the
nature of the ocean. Currents, sun light, stars, seagulls, westerly’s. Know the
boat and know water and know the captain and crew and set sail for a foreign
land. There will be perils and victories but when you control you, you will
reach shore.
C plus is not C. It looks like this.
#include <iostream>
using
namespace std;
int
main()
{
cout << "Hello world!" << endl;
return 0;
c
C plus is deceptively similar to c. The
grammar is different and the coding style is object oriented and not procedure
coded like c and assembly language, Here lets create a
function.
#include <iostream>
using
namespace std;
int
firstfunc (int x, int y);
int
main()
{
int x = 2;
int y = 2;
cout << "Hello world!\n" <<
firstfunc(x, y) << endl;
return 0;
}
int
firstfunc (int z, int y) {
int
x;
x = z * y;
return
x;
}
Lets
see a reference. Classes example. Classes put data and
variables together and functions that manipulate those data member.
#include <iostream>
using
namespace std;
class
Rectangle {
private:
int width, height;
public:
void set_values (int,int);
int area() {return width*height;}
};
void
Rectangle::set_values (int x, int y) {
width = x;
height = y;
}
int
main () {
Rectangle rect;
rect.set_values (3,4);
cout << "area: " << rect.area();
return 0;
}
Ok lets dumb it
down so that we can see this complicated shit work.
// classes example
#include <iostream>
using
namespace std;
class
Rectangle {
private:
int width;
public:
void set_values (int);
int area() {return width;}
};
void
Rectangle::set_values (int x) {
width = x;
}
int
main () {
Rectangle rect;
rect.set_values (3);
cout << "area: " << rect.area();
return 0;
}
Lets
point to object.
// classes example
#include <iostream>
using
namespace std;
class
Rectangle {
//private:
// int width;
public:
int width;
void set_values (int);
int area() {return width;}
void print() {cout << width << endl;}
};
void
Rectangle::set_values (int x) {
width = x;
}
int
main () {
Rectangle rect, *ptrRect = &rect, &refRect = rect;
rect.set_values (3);
rect.print();
rect.width = 7;
cout << "area: " << rect.area();
ptrRect->width = 10;
cout << "area: " << rect.area();
refRect.width = 11;
cout << "area: " << rect.area();
return 0;
}
expression can be read as
*x pointed
to by x
&x address
of x
x.y member y of object x
x->y member y of object pointed to by x
(*x).y member
y of object pointed to by x (equivalent to the previous one)
x[0] first object pointed to by x
x[1] second object pointed to by x
x[n] (n+1)th object pointed to by x
The use of classes
#include <iostream>
using
namespace std;
class
Time {
public:
Time();
void setTime(int, int, int);
void printMilitary();
void printStandard();
private:
int hour;
int minute;
int second;
};
Time::Time(){hour = minute = second = 0;}
void Time::setTime(int h, int m, int s){
hour = (h >= 0 && h < 24 ) ? h : 0;
minute = (m >= 0 && m < 60) ? m : 0;
second = (s >= 0 && s < 60) ? s : 0;
}
void Time::printMilitary(){
cout << (hour < 10 ? "0"
: "") << ":"
<< (minute < 10 ? "0" : "" ) << minute;
}
void Time::printStandard(){
cout << ((hour == 0 || hour == 12) ? 12 : hour % 12)
<< ":" << (minute < 10 ?
"0" : "") << minute
<< ":" << (second < 10 ?
"0" : "") << second
<< (hour < 12 ? "AM" : "PM");
}
int
main() {
Time t;
cout
<< "The initial military time is ";
t.printMilitary();
t.printStandard();
return
0; }
Programming OS Specific
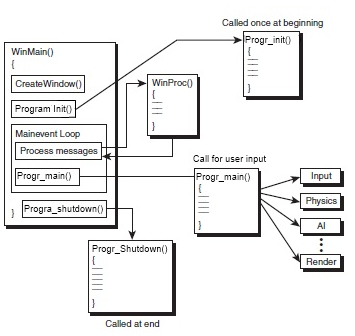
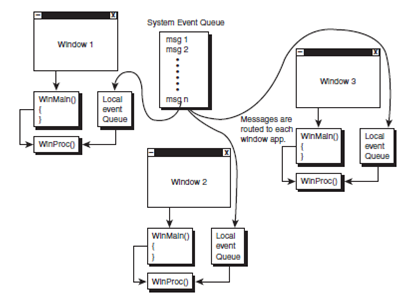
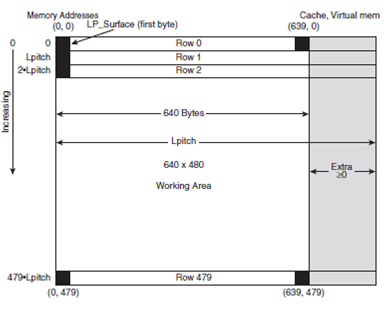
Operating system
Systems are defined as definable separate
parts working together as part of a whole. The operating system is the main
board of all the soft subsystems that run to maintain the integrity, usability,
and conveyance of the computer as a tool. It presents the computer hardware
resources as a monolithic object with hooks, interfaces and services for client
applications or programs. Process, file, memory, and device are the main
control feature of the operating system or OS. The CPU, memory and device
hardware are abstracted by the OS into logical interfaces for client host
programs. The cpu cycles continuously and these cycles
are fed by os governed inputs of process data. Files are the logical chunks at
which data is fed into process. Memory circuity is the cycle pathway. Devices
are other channels and rivers of cycle pathways.
The Forth State of Matter
Have you experienced a balloon unpop, or
light not shined or two objects occur in the same place at the same time. You
have if you are a mathematician or a physicist. These occurrences are predicted
by the language of mathematic and the express experimentation based on that
maths in laboratory experiments. No balloons don’t unpop
but antiparticles are their positives moving backward in time mathematically
speaking and light won’t shine at the most sever space time curvature of a dark
star and lastly forces are boson particles which are perfectly happy being
anywhere in space time and locality. This is the stuff of reality and there is
a little-known analogy between electromagnetism and gravity which is derived
from the fact that they're both vector field functions. James Clerk Maxwell was
the first to derive equations for the divergence and curl of the vector field
these equations became famously known as Maxwell's equations which are the
foundation of conventional electromagnetic theory of the Delta operator which
is designated as an upside down triangle is called a gradient which basically
describes the direction of greatest change in the vector field and the
diversions tells us the amount by which changes when we move in this direction.
The divergence which is designated by a gradient dot product
operator with the delta triangle with a period next to it. The curl is
designated by a cross product which is the X the Delta operator followed by an
X. Electromagnetism breaks consists of the electric field and magnetic field
components.
Einstein’s Gravity
There are four different flavors of
gravity. Einstein’s is expressed in our science as a balance of space, time
with respect to mass and energy. It is observed as the curvature which creates
the cosmic tree like structure in our known universe. This gravity bends space.
Gravity also distorts time. Mass disturbs the gravitational field like a fabric
and warps time and light. The two other forces in the gravity family like
forces, are best described as distortions we have measured as dark matter/dark
energy(a mis nomer) and completely simplistic description as the two are
actually one boson like particle which spans in influence on more than one
dimension which we interpret as missing mass and as we are not outfitted with
uniforms to travel too nor apparatus to experiment on currently, and must
describe it currently as two different phenomena in our computer simulation of
the Universe. The last flavor of gravidity is mediated by what we have described
theoretically as a graviton bosonic particle. The last gravity bosonic particle
has two different properties observed in nature. Gravity as a field can be
described as having gravi-electric and gravi-magnetic components. The fields
are analogous in that just as magnetism is a relativistic induced forced caused
by the movement of electric charge to charge Q and moving through space at this
density and it will produce a magnetic field which curls around the loop of
wire and a corkscrew the direction of the magnetic field is determined by using
the right-hand rule.
The righ-hand rule describes in which
direction electricity or magnetic flux will flow. If you run current through a
wire the motion of the electrons passing through the wire will produce a
magnetic field around the wire. If you take your right hand and point your
thumb in the direction of the current and are electrons move in the direction
of your thumb. They produce a magnetic field in the direction in which your
fingers curl. A coil of wire, tracing the movement of the electrons passing
through it and using the right-hand rule, the magnetic field all add up to a
product which is a single large magnetic field. The presence of charge creates
an electric field and the presence of mass produces a gravity field which its
force carrier we describe as the gravitino or the forth gravity. The motion of
an electric charge through space produces a magnetic field and the motion of a
mass gravi-magnetic field.
Magnetic Propulsion vs Anti-Gravity
Propulsion
Strong magnetic fields can levitate
objects but the fields must oscillate back and forth to achieve this. These unidirectional fields produce rotation
which needs to be stabilized to produce lift.
A superconductors can levitate objects in a
constant magnetic field due to the Meissonier effect, which is a result of
diamagnetism. Which is a form of magnetism that is only
exhibited by a substance in the presence of an externally applied magnetic
field. Super conductors and super fluids are both examples of those
Einstein condensate switches, or the fifth state of matter. A superconductor
conducts electricity with zero resistance quality superfluid flows through a
container with zero resistance friction is totally illuminated a superfluid
will pour straight through ceramic container because of the spores. It will
also flow through the tiniest hole instantly because all the atoms in the
superfluid reduced to a single wave function obeys those Einstein Bose
Einstein's statistics rather than Ferminonic statistics. The Pauli exclusion
principle states that no two atoms or fermions are matter particles can occupy
the same space at the same time the atoms in a Bose Einstein condensate become
bosons or force particles which do not obey the Pauli exclusion principle and can,
when contained, all fit through the tiniest perforation of a container at the
same time if there was an opening wide enough to let one through they could all
fit through at the same time.
In the first quarter of the 19th
century a remarkable discovery was made which changed forever modern
engineering. Governments had acquired an energy reactor technology used for
propulsion which operated on a field which was not completely
electromagnetic nor energetic like thrust created by combustion. Reverse
engineering revealed that a distortion in the first gravity could be created by
a gravity distortion generator which induced a perpetual gradient in a right
handedness relative to the system. The propulsion system used electromagnetic
forces induced by the gravi-electric/magnetic reactor but used gravitational
propulsion as its primary thrust. The engineering principles have been reverse
engineered using fifth state materials. As the original system used materials
of which are unobtainable at this point in human history.
Gravity, mass and light are interrelated.
Light bends when under the influence of gravity. Stars are visible behind the Sun that are blocked from view by
the some reason we can see them is because the sun is a tremendous
gravitational field and it's bending the light around it to the extent that we
can see the stars behind it. Space-time and gravity are all essentially
interrelated they all act on one another. Gravity bends space and gravity also
distorts time. When one is altered you essentially alter the other two. If for
example, one were to have a massive body, it generates gravity producing a lot
of gravitational waves that he will the distorts space
and will the distorts space and space too.
Traveling at the speed of light, without
warping space, is not possible theoretically speaking. At the speed of light
there are several navigational problems. The fact that as your speed increases
so does your mass proportionally. The more energy you put into going faster
begins to slow you down because your velocity energy is converted into mass.
Also, traveling at extreme velocity are fraught with navigational problems
related to collision with little tiny micrometeorites. At speeds like this it
would undoubtedly destroy your ship. Aside from these facts, the amount of
energy required to accelerate to the speed of light is proportional to the
total mass of the system in this case, the Universe.
The system used an isotope of a rare
laboratory element called Element X at the top of the reactor. The base of the
reactor is a small particle accelerator. A particle is accelerated the
high-speed and then deflected up a small tube and it's aimed at element X. This
transmutes the element which causes it a radiation emissions previously never
discovered. It produces an anti-matter particle, which is guided down a tube
and reacts with a plasma gas. When matter and antimatter reactivate convert to
100% efficient energy. Which was a violation of the first law of
thermodynamics? The only byproduct was electrical power in the emitted by the
reactor which powered other subsystems. The sub systems had no apparent wiring
or power. Later, it was discovered that the systems housing was replete with
nanotubuals at the molecular scale. So there was no need for external navigational
power as it is supplied as a byproduct of the reactive reactor, which primary
function was to produce a gravitational bow wave. This bombarded of element X
produced a gravitational wave which was present at the top of the reactor and
projected. Relativistic speed rotation was the source of the gravitational
distortion. Could scientist reverse engineer these properties on earth? We did.
Rotating superconductors produced
gravi-magnetic fields larger than predicted by modern quantum mechanics. This
phenomenon is described by paper written by Russian researcher Eugene
Podkletnov. Similar studies proved by Vienna Austria by Martin Hofmann in a
paper titled gravi-magnetic field of a rotating superconductor. Also, in
American physicist Ning Li and Douglas Torr of the University of Alabama have
described these fields created by super fluids independent of the government.
In order to achieve gravitomagnetic
propulsion, mercury doped ionized phased plasma gas, which is super cooled 150°
Kelvin and pressurized to 200,000 atmospheres and rotated 60k revolutions per
minute. It is a superfluid and a Ferro fluid. At this point the fluid becomes a
Bose Einstein condensate fluid rotating around a container with zero friction
which never slows down. It is propelled electromagnetically to relativistic
speeds. These speeds ionize the gas generating a gravi-magnetic radiation field
perpendicular to the ion spin axis. Back engineering the original system proved
problematic as there were problems with rotating a superfluid because there is
no friction rotating the container. Superfluids by themselves do nothing in a
container because fluids move relative to a container because of adhesion to
the sides of the container. There is no friction force with a superfluid.
Stirring a superfluid achieves no affect as it only makes the atoms rotate on
their individual accesses and doesn't make the fluid rotated as a whole. The
breakthrough came by introducing a Ferro magnetic fluid which will move in the
presence of a magnetic field thus allowing it to rotate the fluid using
electromagnets. The result is the superfluid antigravity centrifuge which has
no limit to how fast the fluid can spin other than the centripetal force that
holds the container together. In order to create lift with the new system, the
craft must have smooth rounded edges to accommodate the rotating superfluid
around the enclosure of the vehicle, like a saucer plate.
The Other Teachers
What Is Higher Learning – What up Cube!
What is a point? Some education professionals
opt out of the definition immediately by saying, a point cannot be defined. The
word point lines and planes are left undefined in order to avoid circularity.
If you say a point is like a dot at the end of a sentence and is infinitely
small. The last statement is the beginning of the brainwashing of higher
learning. Not because the name was changed from point to dot, but now its
purpose was subtly converted from a concept into a physical reality or a marker
location. This double talk puts the listener into a highly suggestive state
psychologically, by turning off cognitive reasoning. It is to say, the fish is
on the hook because, and if you say that each point in a plan is now a location
on the Cartesian plan and now an ordered pair in a Cartesian plane. You have
confounded the meaning to be a mathematic description. If you
explain a dot as a location and construe it as a space time event and as a
figure, like saying the point of impact. Education professionals are
trained to teach a curriculum that thwarts common sense by blending several
conflicting concepts and definitions. If a dot can be a dot
location an ordered pair and an event. Then what is to be said of a dot?
The truth is, a point is a dot. A
geometric figure with the single property of shape. It can be utilized scientifically because it
is a constant form representation cue to the user of a singularity. A location
is an abstract concept. A location does not have a shape. An ordered pair is a
set of instructions to find a dot and an event is the collision of two dots.
The use of the word point as a dot as a location and as an object and as a
concept conflates their respective purposes.
The main purposes of higher learning, is to
support the democratic class system. Democracy is a class system with a buy in
clause. Education, social rank, popular behavior, racial and cultural
classification, social status and most importantly wealth are points toward the
citizen being presented the full suite of freedoms that a social governance
system has to offer.
….UNTIL LATER.
WHO ARE THE OTHER TEACHERS